1. Геометрия
  2. Площадь диагонального сечения

Площадь диагонального сечения прямоугольного параллелепипеда равна 400см2;
стороны основания равны 12см и 16см. Вычисли объём.

st1rb1t st1rb1t    1   08.04.2020 13:13    0

Ответы
Floki23 Floki23  12.10.2020 22:35
Решение:

Найдём диагональ, чтобы затем найти высоту данной фигуры, поскольку объём прямоугольного параллелепипеда равен произведению длины, ширины и высоты.

\sqrt{DA^2+DC^2}=\sqrt{12^2+16^2}=\sqrt{144+256}=\sqrt{400}=20 (см).

Теперь, исходя из первого объяснения, найдём высоту данной фигуры для того, чтобы выполнялись формула объёма прямоугольного параллелепипеда.

DD_1=\cfrac{400}{20}=20 (см).

Теперь, следуя формуле, найдём объём прямоугольного параллелепипеда.

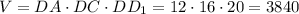V=DA \cdot DC \cdot DD_1=12 \cdot 16 \cdot 20=3840 (см³).

ответ:   \boxed{\bf 3840} (см³).
Площадь диагонального сечения прямоугольного параллелепипеда равна 400см2; стороны основания равны 1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
DinaraBergeneva DinaraBergeneva  20.05.2019 23:10
Боковое ребро и высота правильной четырехугольной пирамиды соответственно равны корень из 34 и 4 см. найдите площадь боковой поверхности пирамиды...
890ZLO168 890ZLO168  20.05.2019 23:10
Всосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. объём жидкости равен 120 мл. сколько миллилитров жидкости нужно долить, чтобы полностью наполнить...
НубИк10 НубИк10  20.05.2019 23:10
Основание равнобедренного треугольника равно 4 см, а боковая сторона - 4,6 см. найдите площадь треугольника....
ykropmen ykropmen  20.05.2019 23:10
Впрямоугольном треугольнике abc (угол c=90 градусов) ab=10см, радиус вписанной в нее окружности равен 2 см. найдите площадь этого треугольника...
baget97ozu06u baget97ozu06u  20.05.2019 23:10
Высота правильной треугольной пирамиды в два раза меньше стороны основания. найдтие угол между боковой гранью пирамиды и плоскостью основания. заранее !...
Nelly175 Nelly175  15.11.2020 14:43
ХЕЛП! Остался час до здачи(( с меня лайк и корона 1. Знайдіть сторону ромба АBCD 2. Площу ромба 3. Висоту ромба хоть что-то...
ПомошницаНомер1 ПомошницаНомер1  15.11.2020 14:43
У коло вписано квадрат зі стороною 6 корень 2 см. Знайдіть сто рону правильного трикутника, описаного навколо цього кола.​...
zaira0 zaira0  18.08.2019 16:30
Дан треугольник авс угол b=90 градусов ас=26 см ав: вс=5: 12 найти: ав,вс...
Ернур150400 Ернур150400  18.08.2019 16:30
Вшколе задали, нарисовать треугольник с 2 тупыми углами. возможно бред. если возможен он то можно фото)...
raykyoko raykyoko  18.08.2019 16:30
Признаки равенства треугольников. три формулировки....

Популярные вопросы