Отрезок ab не пересекает плоскость альфа. прямые ac и bd, перпендикулярны этой плоскости, пересекают ее в точках c и d соответственно. bd=14 см, ac=34 см? cd=15 см. найдите ab.
Другие вопросы по теме Геометрия
Популярные вопросы
- Окаких событиях великой отечественной воины повествуют стихотворные отрывки: и ты...
3 - Фонетический,морфемный,морфологический разбор слова удоляющегося...
1 - 1)для функции у=ixi найдите наименьшее значение на отрезке [-2 ; 1] 2)какое из предложенных...
1 - Проверочные слова к словам тетучий,соловей,молоко....
2 - Сочинение-рассуждение раскрывая смысл высказывания известного писателя л .н толстого:...
2 - Ливонская война таблица основных событий...
1 - 20. укажи в каких случаях верно определенна часть речи. маленький-прилаг. яблоко...
1 - Почему земское движение конца 70-х гг. не принесло ожидаемых результатов и постепенно...
3 - Как решить уравнение 0.8(x-1.9)=0.56? ?...
3 - Сочинение на тему сравнительная характеристика двух людей(друзей одноклассников).помигите...
2
Сделаем дополнительное построение, проведём из точки В перпендикуляр ВК.
Треугольник АВК прямоугольный
по теореме Пифагора найдем АВ=√ВК²+АК²
ВК=ВD=15 cм, т к ВКDC прямоугольник
АК=АС-CD=34-14=20 см
АВ=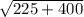 =
= 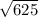 =25 см
=25 см
ответ АВ=25 см
ABDC - прямоугольная трапеция, из В опусти на АС перпендикуляр ВН. тогда BDCH - прямоугольник, и АВН - прямоуг. треугольник. НС = BD, НС = 14. АН = АС - НС; АН = 34 - 14 = 20. BH = CD, BH = 15. Теперь по теореме Пифагора найдем гипотенузу треугольника АВН . АВ = \sqrt{BH^2 + AH^2} = \sqrt{225 + 400} = \sqrt{625} = 25
ответ: 25 см
1. Свойство перпендикулярных прямых гласит, что если две прямые перпендикулярны друг другу, то перпендикуляр, опущенный из любой точки одной прямой на другую прямую, является кратчайшим отрезком между этими двумя прямыми.
2. Свойство прямой, проходящей через пересечение плоскости и прямой гласит, что такая прямая будет пересекать плоскость под тем же углом, под которым она пересекает плоскость с перпендикулярной прямой.
Итак, давайте решим задачу:
Пусть точка O - точка пересечения прямых ac и bd. Так как ab не пересекает плоскость альфа, а прямые ac и bd перпендикулярны плоскости альфа, то отрезок cd является высотой равнобедренного треугольника aOc и bOd, проведенной на основание ab. Таким образом, мы можем сказать, что треугольники aOc и bOd прямоугольные.
Зная, что bd = 14 см, ac = 34 см и cd = 15 см, мы можем использовать теорему Пифагора для нахождения длины отрезка ab.
В треугольнике aOc:
aO^2 + Oc^2 = ac^2 (теорема Пифагора)
aO^2 + 15^2 = 34^2
aO^2 = 34^2 - 15^2
aO^2 = 1156 - 225
aO^2 = 931
aO = √931 (извлекаем квадратный корень)
Аналогично, в треугольнике bOd:
bO^2 + Od^2 = bd^2
bO^2 + 15^2 = 14^2
bO^2 = 14^2 - 15^2
bO^2 = 196 - 225
bO^2 = -29
bO = √(-29) (квадратный корень из отрицательного числа не определен)
Поскольку bO равен отрицательному числу, мы не можем найти его значение. Это означает, что отрезок ab не существует или некорректно задан.
Таким образом, ответ на задачу: отрезок ab не существует или некорректно задан.