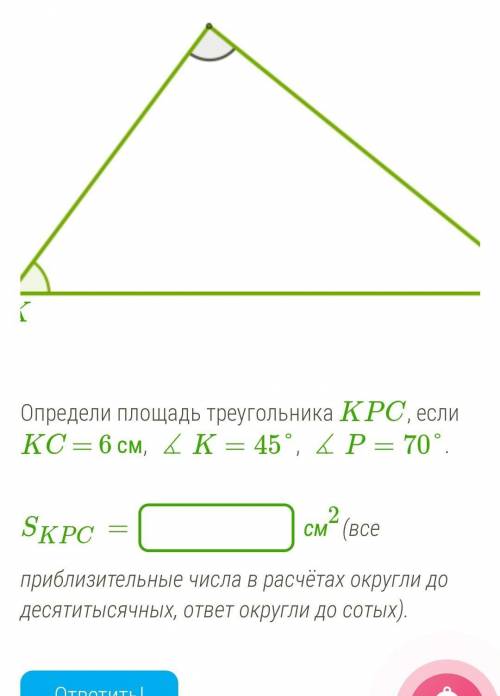
Определи площадь треугольника KPC, если KC = 6 см, ∡K=45°, ∡P=70°.
Другие вопросы по теме Геометрия
Популярные вопросы
- Переведите 4 7/9 в десятичную дробь...
3 - на клетчатой бумаге с размером клетки 1х1 отмечены точки A, B, C, D....
1 - 02зустрічається в природі у вигляді:оксидів:простої речовини,сульфідів...
1 - Алгебра 7. Функція задана формулою у = kх + 3. для яких значень k графік...
2 - Найдите в тексте сложные слова и определите их вид (на казахском)Только...
2 - Чому римський історик писав, що Август отримав Рим цегельним, а залишив...
1 - Г 6. У Алии и Тимура есть по 5000 тенге. Что каждый из них можеткупить...
2 - Радіус кола описаного навколо прямокутного трикутника 4,3 см знайди...
3 - Який обєм іоди потрібно додати до 45 г оцетовойі есенційі (80%)щоб...
1 - Запишіть координати точки, що симетрична точці В(-7; 5;3) відносно...
3
Формула для площади треугольника: S = (1/2) * a * b * sinC
Где:
- S - площадь треугольника,
- a и b - длины двух сторон треугольника,
- C - угол между этими сторонами.
В данном случае, у нас есть сторона KC длиной 6 см, угол K равен 45° и угол P равен 70°.
Для начала, мы можем найти сторону PC, используя теорему синусов. Теорема синусов гласит:
a/sinA = b/sinB = c/sinC
Где a, b, c - стороны треугольника, A, B, C - соответствующие им углы.
Теперь подставим имеющиеся значения:
KC/sinP = PC/sinK
6/sin70° = PC/sin45°
PC = (6 * sin45°) / sin70°
Вычислим это:
PC = (6 * 0.707) / 0.9397
PC ≈ 4.242 / 0.9397
PC ≈ 4.520 см
Теперь, имея длины сторон KC и PC, мы можем использовать формулу для площади треугольника:
S = (1/2) * KC * PC * sinP
S = (1/2) * 6 * 4.520 * sin70°
Вычислим это:
S = (1/2) * 27.12 * 0.9397
S ≈ 12.7705 см²
Итак, площадь треугольника KPC составляет приблизительно 12.7705 см².