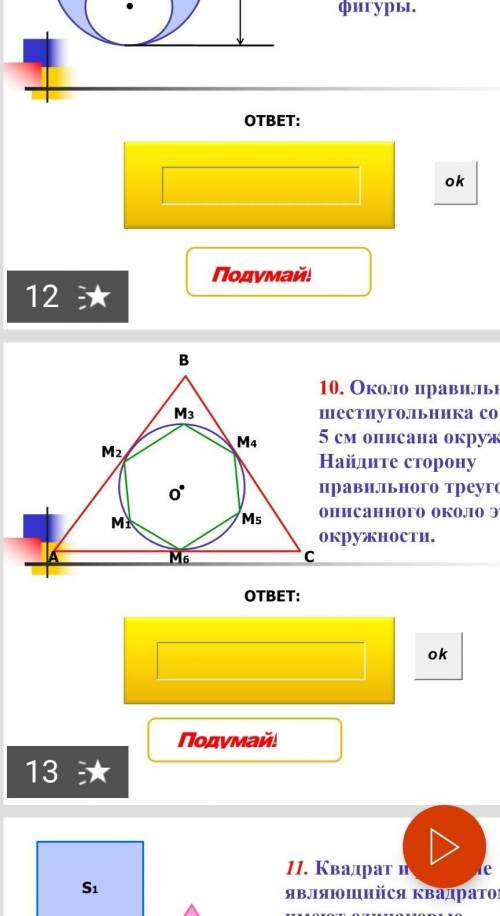
около правильного шестиугольника со стороной 5 см описана окружность. найдите сторону правильного треугольника, описанного около этой окружности ​

правильный треугольник -это равносторонний треугольник

радиус описанной около него окружности равен

r=(a*корень из 3)/3 а -сторона этого треуг-ка

r=(5*корень из 3)/3

сторона правильного шестиугольника будет равна радиусу этой окружности т . к. сторона правил-го 6-ка равна радиусу описанной около него окруж-ти

Для решения этой задачи нам понадобятся некоторые свойства правильных многоугольников.

1. Во-первых, у правильного треугольника все стороны равны.
2. Во-вторых, расстояние от центра окружности, описанной около правильного многоугольника, до любой его стороны равно радиусу этой окружности.

Для начала, найдем радиус окружности, описанной около правильного шестиугольника. Для этого воспользуемся формулой:

радиус = сторона / (2 * sin(180° / количество сторон)).

В нашем случае количество сторон шестиугольника равно 6, а сторона равна 5 см.

Рассчитаем радиус:

радиус = 5 см / (2 * sin(180° / 6)) = 5 см / (2 * sin(30°)) = 5 см / (2 * 0.5) = 5 см / 1 = 5 см.

Теперь у нас есть радиус окружности, описанной около шестиугольника. Заметим, что сторона правильного треугольника, описанного около этой окружности, является диаметром этой окружности. Для того чтобы найти диаметр, умножим радиус на 2:

диаметр = 2 * радиус = 2 * 5 см = 10 см.

Таким образом, сторона правильного треугольника, описанного около окружности, описанной около правильного шестиугольника со стороной 5 см, равна 10 см.