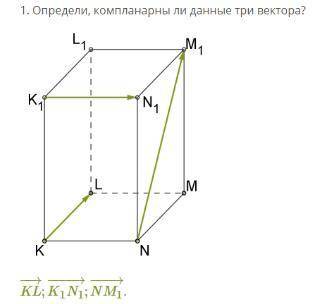
Определи, компланарны ли данные три вектора?
KL−→;K1N1−→;NM1−→.
ответ:
да
нет
2. Подбери нужное слово, чтобы получить правильное суждение о векторах.
1) Если два вектора расположены на параллельных прямых, то они .
2) Если три вектора расположены в одной плоскости, то они .
3) Для сложения трёх некомпланарных векторов применяют закон
Другие вопросы по теме Геометрия
Популярные вопросы
- 10 тез на тему розмаїття сучасної лірики...
3 - Используя данные графика, оцените влияние фитогормонов на рост...
3 - Обернений процес згорання палива...
3 - с алгеброй построение графиков обязательное если нужно! 1)-х²=8/х...
2 - Составьте сочинение на тему описание друга...
3 - написать сочинение 1. Моё отношение к Герасиму. 2. Кто такой Герасим?...
1 - Отзыв на рассказ В. Карасева новогодний подарок...
3 - Раскройте скобки и поставьте глаголы в нужном времени, укажите...
2 - Практическая работа. Тема. Функциональная сердечно-сосудистая проба....
3 - 12. Уявіть, що друг чи подруга зацікавилися справою, яку ви подобляете...
1
1. Определим координаты каждого вектора.
Для вектора KL−→, координаты могут быть обозначены как KL(x1, y1, z1).
Для вектора K1N1−→, координаты могут быть обозначены как K1N1(x2, y2, z2).
Для вектора NM1−→, координаты могут быть обозначены как NM1(x3, y3, z3).
2. Составим систему уравнений, используя координаты векторов.
Так как требуется определить, компланарны ли вектора, мы можем использовать систему линейных уравнений следующего вида:
a(x1 - x2) + b(y1 - y2) + c(z1 - z2) = 0
d(x1 - x3) + e(y1 - y3) + f(z1 - z3) = 0
3. Решим систему уравнений.
Решение системы показывает, что уравнения имеют единственное или бесконечное количество решений. Если система имеет единственное решение, то вектора KL−→, K1N1−→ и NM1−→ являются некомпланарными. Если система имеет бесконечное количество решений, то вектора KL−→, K1N1−→ и NM1−→ являются компланарными.
4. В данном случае наша система имеет бесконечное количество решений.
Это означает, что вектора KL−→, K1N1−→ и NM1−→ являются компланарными.
Теперь давайте ответим на вторую часть вопроса, подберем нужные слова для правильного суждения о векторах:
1) Если два вектора расположены на параллельных прямых, то они коллинеарны.
2) Если три вектора расположены в одной плоскости, то они компланарны.
3) Для сложения трех некомпланарных векторов применяют закон параллелограмма.
Таким образом, ответ на вопрос будет таким:
1) да
2) компланарны
3) параллелограмма.