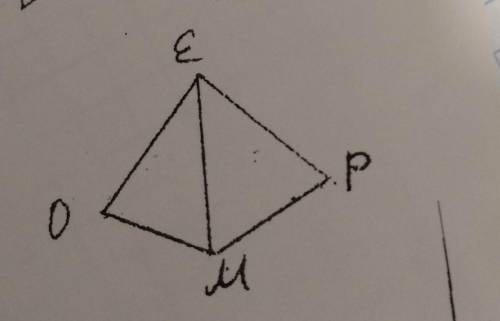
OM=MP
OE=PE
Доказать,что EM -биссектриса угла OEP​

Для доказательства того, что EM является биссектрисой угла OEP, мы можем использовать свойство биссектрисы, которое гласит, что биссектриса угла делит данный угол на две равные части.

Прежде чем начать доказательство, давайте вспомним, что биссектриса - это линия, которая делит данный угол на два равных участка. Она проходит через вершину угла, и каждая из двух половин угла равна другой.

Теперь вернемся к нашей задаче. У нас имеется треугольник OEP, где OM = MP и OE = PE. Нам нужно доказать, что EM является биссектрисой угла OEP.

Давайте рассмотрим два треугольника: треугольник OME и треугольник PME. У нас есть две равные стороны: OM = MP и OE = PE. Также у них есть общая сторона ME.

По свойству равенства треугольников (ССС), мы можем сделать вывод, что треугольники OME и PME равны друг другу.

Таким образом, углы OME и PME также равны друг другу. Обозначим их α.

Теперь обратим внимание на угол OEP. Он равен сумме углов OME и PME. То есть, угол OEP = α + α = 2α.

Но мы знаем, что треугольник OME равен треугольнику PME, поэтому углы OME и PME равны. Это означает, что α = α.

Теперь вернемся к углу OEP. Мы сказали, что он равен 2α. Если α = α, то угол OEP = 2α = 2α.

Таким образом, мы доказали, что угол OEP можно разделить на две равные части, и EM является его биссектрисой.

В итоге, по указанным равенствам и свойству равенства треугольников мы доказали, что EM является биссектрисой угла OEP.