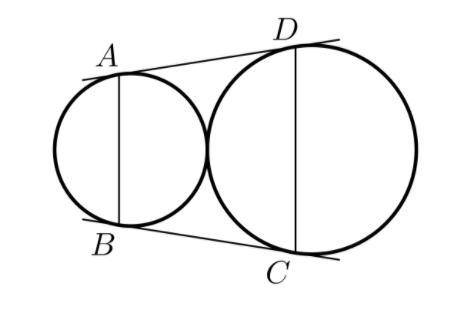
Окружности ω1 и ω2 касаются друг друга внешним образом. Их общие внешние касательные касаются ω1 в точках A и B, а ω2 — в точках D и C соответственно. Известно, что AB=8, CD=13. Чему равна длина отрезка BC?
Другие вопросы по теме Геометрия
Популярные вопросы
- Юннаты высадили 80 саженцев тополя,саженцев дуба в 2 раза больше,чем...
3 - Описание людей (внешность, характер, личностные качества, профессия)...
1 - Перевести , хоть немного ата – бабамыздың ежелден келе жатқан игi дәстүрлерiнiң...
1 - Можно ли по внешнему виду различить растения влажных мест и засушливых...
2 - Сколько оборотов делает земля в вокруг своей оси за целый год...
3 - 2класс: какие птицы относятся к ловчим?...
2 - Прочитай статьи из словаря синонимов почему о луне говорят диск серп...
2 - Представьте в виде дроби 18m3\11n3. 22n4\9m2...
1 - Развития каких наук требовала сама жизнь в египте?...
3 - Га уроке физкультуры оле дали пробежать 300 /тысячных километра а лене...
2
Пусть AD и BC пересекаются в точке E.
Отрезки касательных из одной точки равны, EA=EB, ED=EC.
△AEB, △DEC - равнобедренные => EAB =90 -E/2 =EDC => AB||DC
ABCD - трапеция
MA=MK=MD, NB=NK=NC (отрезки касательных из одной точки)
MN - средняя линия трапеции ABCD
MN =(AB+CD)/2 =(8+13)/2 =10,5
NB=NK=NC => NK=BC/2
Центры лежат на биссектрисе угла E (т.к. окружности вписаны в угол).
Точка внешнего касания окружностей K лежит на линии центров, то есть на биссектрисе угла E.
MN||AB => △MEN~△AEB =>
△MEN - равнобедренный, EK - биссектриса и медиана, NK=MN/2
BC =MN =10,5