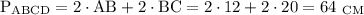Одна із сторін паралелограма дорівнює 12 см, більшa діагональ - 28 см, а тупий кут - 120 градусів. знайти периметр паралелограма.
Другие вопросы по теме Геометрия
Популярные вопросы
- Значение животных для природы 7-10 примеров,и роль животных для человека...
3 - Выполни действия 1) 10м3см-7дм8см 2) 36мин27с+40мин53с 3) 9т4кг-37ц85кг...
2 - Напишите какая польза и вред есть в царстве !...
3 - Подскажите а какая буква пропущена н зина...
3 - Периметр прямоугольного треугольника равен 80 см. а катеты относятся как...
3 - Запишите все двузначные числа в запись которых лишь цифры 2 и 3 . найдите...
2 - Запишите все четырехзначные числа, состоящие из цифр 1,2,3,4. сколько чисел...
3 - Решить 4 1/3 : (5/6+0,25) 3,6*(7/12+1/9) (7/12-2/15): 0,9 (5/8-1/3)*1 5/7...
3 - Масса двух гусей 11,5 килограмм. чему равна масса каждого гуся,если масса...
1 - Распределить слова с орфограммами гласных по группам: корень, приставка,...
3
Пусть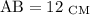 и
и 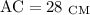 . Из условия
. Из условия 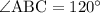
По теореме косинусов:
Периметр параллелограмма: