Объем цилиндра,у которого высота вдвое больше диаметра основания, равен 1м^3. Вычислите его высоту. а)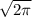 см б)
см б)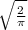 см в)2
см в)2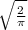 см решить!! Очень нужно
см решить!! Очень нужно
Другие вопросы по теме Геометрия
Популярные вопросы
- Число а кратно 7.служит ли число 7 делителем числа 15а? делителем числа...
2 - Что не найти север? а.по полярной звезде. б.по полуденной тени. в.по...
2 - Не могу понять как пишется шишлычок или шышлычок или подругому?...
2 - Главные герои ивана сусанина и их тембры голосов?...
1 - На миниатюре 13 века изображён христос вручающий ключ папе римском...
1 - Вычислить среднюю скорость лыжника путь 15 км за 1 ч 23 мин 20 с...
1 - Обязательно укажи каковы особенности лета в пустыне какие растения...
1 - Барбикен защищая свою идею говорил о тех фантазерах которые пускались...
1 - ответь на вопрос: кто создал человека,согласно и мифам древних народов?...
2 - 1га деревьев и кустарников в течение 1 ч поглощают столько углекислого...
1
V = π * r^2 * h,
где V - объем цилиндра, r - радиус основания и h - высота цилиндра.
Поскольку высота цилиндра в два раза больше диаметра его основания, то можно записать:
h = 2 * r,
где r - радиус основания.
Теперь мы можем заменить h в формуле для объема цилиндра:
V = π * r^2 * (2 * r).
Из условия задачи мы знаем, что V = 1 м^3.
Теперь мы можем записать уравнение и решить его:
1 = π * r^2 * (2 * r).
Избавляемся от множителя π:
1 / π = 2 * r^3.
Делим обе части уравнения на 2:
1 / (2 * π) = r^3.
Находим кубический корень от обеих частей уравнения:
∛(1 / (2 * π)) = r.
Таким образом, радиус основания цилиндра равен ∛(1 / (2 * π)).
Теперь мы можем найти высоту цилиндра, подставив значение радиуса в формулу для h:
h = 2 * ∛(1 / (2 * π)).
Округлим ответ до двух значащих цифр и запишем его в нужной единице измерения (сантиметрах).
Таким образом, ответом является вариант б), который записывается как 2 * √(2/π) см.