( ) Нужно развёрнутое объяснение выполнения этих задач.

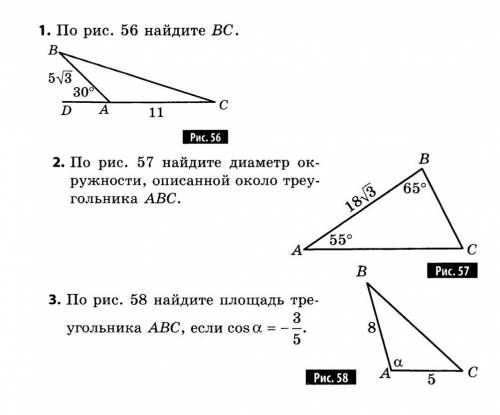
1. 1) Проведем ВD перпенд. АС.

2) В прямоуг. тр. BDA:

- BA (гипотенуза)=5sqrt(3)

- <BAD=30°

=> BD (катет напротив угла 30°) = 5sqrt(3)/2.

3) Найдем DA по Пифагору:

sqrt(75-18.75)=sqrt(56.25)=7.5.

4) DC = 11+7.5=18.5

5) BC по Пифагору:

sqrt(18.75+342.25)=sqrt(361)=19.

ответ: 19.

2. 1) <С=60°.

2) По т. синусов:

a/sin(A)=b/sin(B)=c/sin(C)=2R.

=> (18sqrt(3))/sin(60°)=36.

36 = 2R => R = 18.

ответ: 18.

3. 1) cos^2(a) + sin^2(a) = 1

=> sin(a) = +-sqrt(1 - cos^2(a))

sin(a) = +-sqrt(1 - 9/25) = +-sqrt(16/25) = +-4/5.

2) Если и косиеус, синус отрицательные, то угол больше 180° (3я четверть окружности), что невозможно => синус положительный => sin(a) = 4/5.

3) Формула площади:

S = 1/2 * a * b * sin (угла между а и b)

S = 1/2 * 8 * 5 * 4/5 = 16.

ответ: 16.