Нужна желательно поподробнее расписать. )) окружности радиусов 27 и 54 касаются внешним образом. точки a и b лежат на первой окружности, точки c и d — на второй. при этом ac и bd — общие касательные окружностей. найдите расстояние между прямыми ab и cd.
Ответы
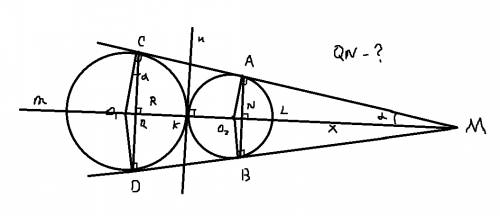
R≡54,r≡27. Пусть # синвол параллельности, ↓ перпендикуляр. R ↓ ac , r ↓ ac ⇒ao2 # co1. (ao2=r , co1=R). o1,o2 ∈ m. Где m=Mo1 и M точка пересечение ac и bd. O1q ↓ cd , O2n ↓ ab. cd # ab. ( cd # n, n↓m ab # n). Значит qn расстояние между ab и cd. Угл cmo2=a ⇒ sin(a)=27/(27+x)=O2n/27 27/(27+x)=54/(108+x). Где x =LM L точка пересечение (o2;r) c m. Sin(a)=O1q/54=O2n/27. Отсюда O2n=9 O1q=18 ⇒ QK=54-18=36. QN= 36+27+9=72. Простите если непонятно писал.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Почему так рассердился Онегин, оказавшись в гостях у Лариных?(Евгений...
1 - С каким из названных вами материков связанны открытия путешественников...
3 - 5/6x=25 найти корень уравнения 8/11х=1...
1 - 2/5*z+2\3*z-7\15 решить уравнение...
3 - Почему сказка премудрый пискарь была так названа?...
2 - Выбери нужное cлово и подбери ответ...
3 - Поставьте глаголы, данные скобках, в со- ответетвующей личной форме...
1 - При прохождении тока силой 1,6A в течение 20 минут через электролитную...
2 - История казахстана СОР 2 Уйсуни и Кангюи 5 класс 3 четв - ПАМАГИТЕ...
1 - Решать без if, !=? while и т.д) Можно через Питон,С++,Джава...
2