Нужна в Геометрии. Желательно с решением и пояснением
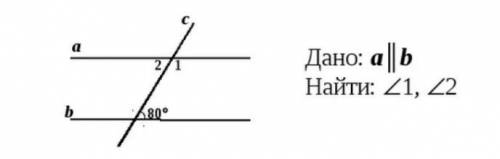
Другие вопросы по теме Геометрия
Популярные вопросы
- Даны 30 г водорода и 50 мл воды (нормальные условия). рассчитайте, в каком из...
1 - Ярешаю летнюю тетрадь будущего четвероклассника а там такие вопросы: почему...
2 - А.с.пушкин руслан и людмила напишите главных героев,момент который вам понравился(кратко)...
2 - Разделите 20 конфет, не разламывая их, между четырьмя подругами так, чтобы каждая...
2 - Катер должен пройти ав со средней скоростью 4 ч. однако первую половину пути...
1 - 5x^2y^2-45a^2b^2 розкласти на множники...
3 - Токарь должен вытачивать каждый день по 15 деталей, если он будет вытачивать...
2 - Точки с,d,e лежат на одной прямой .длина отрезка de в 2 раза меньше длины cd...
1 - На строительстве стены первый каменьщик работал 5 дней один. затем к нему присоединился...
1 - Запиши однокоренные ответы с приставками к слову посвистывать...
2
надеюсь понятно объяснила
Объяснение:
сумма улов равна 180
180-80=100
поэтому угол 1=100, а угол 2=80
На данной картинке изображен треугольник ABC, в котором AB = 5 см, BC = 7 см и AC = 8 см. Задача состоит в том, чтобы найти высоту треугольника, проведенную из вершины B на сторону AC.
Для решения этой задачи мы можем использовать теорему Пифагора и формулу площади треугольника.
1. Давай начнем с использования теоремы Пифагора. Эта теорема гласит, что в прямоугольном треугольнике квадрат гипотенузы (стороны напротив прямого угла) равен сумме квадратов катетов (других двух сторон).
В нашем случае треугольник ABC не является прямоугольным, но мы можем создать вспомогательный прямоугольный треугольник, опирающийся на сторону AC. Для этого мы проведем высоту BH.
2. Теперь, применяя теорему Пифагора к прямоугольному треугольнику ABH, можем записать:
AB^2 = AH^2 + BH^2.
Заметь, что мы обозначили высоту треугольника как BH и гипотенузу как AB.
3. Значение AB мы знаем из условия задачи - AB = 5 см. Таким образом, у нас есть:
(5 см)^2 = AH^2 + BH^2.
Выразим теперь BH из этого уравнения:
BH^2 = (5 см)^2 - AH^2.
4. Далее нам необходимо найти AH - высоту треугольника. Мы можем сделать это, используя формулу площади треугольника.
Площадь треугольника можно выразить как половину произведения длины стороны на длину проведенной к ней высоты:
Площадь ABC = (1/2) * AC * BH.
Нам известны значения сторон треугольника ABC: AB = 5 см, BC = 7 см и AC = 8 см. В задаче не указана площадь треугольника, поэтому мы не можем продолжать дальше, пока не найдем значение высоты.
5. Давай поищем другой путь для решения задачи. Обратимся к понятию "подобных треугольников". Мы можем заметить, что треугольник ABC и треугольник BHA подобные, потому что у них одинаковый угол при вершине B (угол ABC).
Для подобных треугольников отношение длин сторон (или высот) равно отношению соответствующих сторон треугольников.
6. В нашем случае, отношение длины стороны BH к длине стороны BC равно отношению длины стороны AH к длине стороны AC:
BH/BC = AH/AC.
Значение длин сторон BC и AC мы знаем из условия задачи: BC = 7 см и AC = 8 см.
7. Подставляя эти значения в уравнение выше, получим:
BH/7 = AH/8.
Теперь нам известны два отношения между BH, BC, AH и AC, и мы можем создать систему уравнений:
(5 см)^2 = AH^2 + BH^2,
BH/7 = AH/8.
8. Решая эту систему уравнений, мы сможем найти значения высоты BH и AH. Подставим второе уравнение в первое:
(5 см)^2 = (8/7 * BH)^2 + BH^2.
9. Теперь решим получившееся уравнение. Раскроем скобки в правой части уравнения:
25 см^2 = (64/49 * BH^2) + BH^2.
10. Приведем подобные слагаемые справа:
25 см^2 = (64/49 + 1) * BH^2.
11. Просуммируем дробь в скобках:
25 см^2 = (64/49 + 49/49) * BH^2.
12. Упростим дробь в скобках:
25 см^2 = 113/49 * BH^2.
13. Умножим обе части уравнения на 49:
25 см^2 * 49 = 113 * BH^2.
14. Раскроем скобки в левой части уравнения:
1225 см^2 = 113 * BH^2.
15. Делим обе части уравнения на 113:
1225 см^2 / 113 = BH^2.
16. Извлекаем квадратный корень из обеих частей уравнения:
√(1225 см^2 / 113) = BH.
17. Получили значение BH:
BH ≈ 10.235 см.
18. Теперь нам нужно найти AH. Мы можем использовать отношение длин сторон BH и BC из уравнения:
BH/BC = AH/AC.
Подставим значения:
10.235/7 = AH/8.
19. Решим уравнение, умножив обе части на 8:
(10.235/7) * 8 = AH.
20. Вычисляем значение AH:
11.74 см.
Итак, высота треугольника BH равна приблизительно 10.235 см, а высота AH равна приблизительно 11.74 см.
Надеюсь, это разъясняет решение данной геометрической задачи. Если у тебя возникнут еще вопросы, пожалуйста, не стесняйся задавать их!