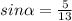Найти синус острого угла а, если cos а = 12/13
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.разкройте скоби: 1) (m^½ - n½)²; 2) (x^1/6 + 2)(x⅓ - 2x^1/6 + 4);...
3 - Чому пучок світла від ліхтарика добре видно в запиленому повітрі?...
3 - Будивелний подъемник за 2 хв пиднимае вантаж на 31 й поверг будинку....
2 - Когда на пружине висят одинаковых груза период свободных вертикальных...
3 - Вирішуйте що знаєте ів будь ласка! !...
3 - Надлежит графику уравнения 3х - 4 + 24 в 0? •3. постройте график...
2 - Мені потрібно есе до твору слово о полку ігоревім . також навести...
1 - 1. перед вами структурные компоненты клетки : аппарат гольджи, вакуоль,...
2 - Перевисти из языка c++ в свот код: #include #include using namespace...
1 - Прочитайте предложения , .исправьте ошибки ,связанные с лексической...
2
5/13
Объяснение:
Используем основное тригонометрическое тождество, а именно
Из неё можно вывести следующую формулу:
Получается следующее:
ответ: