1. Геометрия
  2. Найти площадь полной

Найти площадь полной поверхности цилиндра с радиусом основания 3 см и дагональю осевого сечения 10 см.

stesha24 stesha24    2   19.03.2021 03:12    1

Ответы
OМайгад OМайгад  18.04.2021 03:53

207,24

Объяснение:

Радиус основания - 3 см, тогда диаметр - 6 см

вычисляем высоту по теореме Пифагора:

(все под корнем)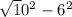 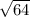\sqrt 10^{2} -6^{2}=\sqrt{64}=8

R=3  h=8

Площадь полной поверхности цилиндра:

S = 2 π R (R + h) = 2π*3*(3 + 8) = 66*3,14= 207.24

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
макс10106 макс10106  08.05.2021 17:15
Рассматривается правильная четырёхугольная пирамида SABCD с основанием АВСD. а)  Изобразите на чертеже рассматриваемую пирамиду и какое-либо её сечение, являющееся четырехугольником....
JuliIs26 JuliIs26  08.05.2021 17:20
Радиус и площадь круга, вписанного в ромб....
sdfxcg sdfxcg  08.05.2021 17:27
Обчисли сторони і площу прямокутника, якщо його діагональ дорівнює 9√3дм і утворює з більшою стороною кут 30 градусів. Більша сторона =... дм.Менша сторона=. ...√... дм.Площа...
fhdjfjfuf fhdjfjfuf  08.05.2021 17:28
 Рассматривается правильная четырёхугольная призма   АВСD A1B1C1D1., М – точка на ребре АВ такая, что АМ = 2 ВМ а)  Изобразите на чертеже рассматриваемую призму  и данную точку...
вафелька6 вафелька6  08.05.2021 17:30
Хорды AB и CD пересекаются в точке 0.Найдите отрезок OD, если A0=6Ова 4 и со 3.​...
Lilu700 Lilu700  08.05.2021 17:31
Рассматривается правильная четырёхугольная призма   АВСDA1B1C1D1. М – середина ребра AD а)  Изобразите на чертеже рассматриваемую призму  и данную точку М. б)   Пусть плоскость...
Marusya2099 Marusya2099  08.05.2021 17:33
Дан треугольник ABC, на стороне AC которого взята точка D такая, что AD=7 см, а DC=9 см. Отрезок DB делит треугольник ABC на два треугольника. При этом площадь треугольника ABC составляет 112 см2....
Vladko1337lol Vladko1337lol  08.05.2021 17:33
Слишком коротко. Напишите как минимум 20 символов, чтобы получить лучший ответ....
tana29143Танечка tana29143Танечка  20.04.2020 11:04
ТОЛЬКО ОТВЕТЫ С РЕШЕНИЕМ УМОЛЯЮ ВАС...
weldys99 weldys99  20.04.2020 11:02
геометрия 8 класс с решение...

Популярные вопросы