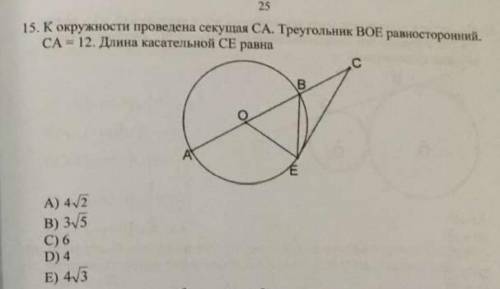
Найти длину касательной СЕ.

Радиус ОЕ перпендикулярен касательной СЕ в точке касания Е, а т.к. ΔВОЕ равносторонний, то ∠ВОЕ=60°, но тогда в прямоугольном треугольнике СЕО ∠ОСЕ=30°, и катет ОЕ=R, лежащий против угла в 30°, равен половине гипотенузы ОС=АС-АО=(12-R) ,  ОЕ=ОВ=ОА=R, тогда

R=(12-R)/2, откуда 3R=12, R=12, R=12/3=4,

Из свойств секущей и касательной известно, что СЕ²=АС*СВ;

СЕ²=12*(12-2R)=12*(12-8)=48, СЕ=√48=4√3

верный ответ Е) 4√3