Найдите значение cos α, если известно значение 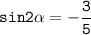
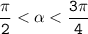
Другие вопросы по теме Геометрия
Популярные вопросы
- Ест по V главе романа А.С. Пушкина «Евгений Онегин» 1. Эпиграфом...
1 - Тест по IV главе романа А.С. Пушкина «Евгений Онегин» 1.Какое впечатление...
1 - ЗДРАВСТВУЙТЕ Частное двух чисел в 12 р. Меньше делимогои в три раза...
3 - Решите задачи: Используя формулу Бернулли: 1) Известно, что из 20...
2 - 1. С целью подготовки детей к написанию цифр предлагается система...
2 - Общага В)Конституция РФ является источником (основой) большинства...
1 - общага1) укажите орган/ органы государства , ограничивающие конституционные...
1 - Найти остаток от деления числа 1415 в 7ричной на число 14 в 12ричной,...
2 - По рассказу А.И. Солженицына Матренин двор написать сочинение -рассуждение...
3 - Как извлечь корень из числа 601?...
1
Надо воспользоваться формулой: sin(2α) = 2*sin(α)*cos(α).
Функцию sin(α) выразим через cos(α).
sin(α) = √(1 - cos²(α)).
Подставим в первое уравнение:
-3/5 = 2*√(1 - cos²(α))*cos(α). Возведём обе части в квадрат.
9/25 = 4*(1 - cos²(α))*cos²(α). Приведём к общему знаменателю и раскроем скобки.
9 = 100cos²(α)) - 100cos^4(α).
Получили биквадратное уравнение. Введём замену: cos²(α) = t.
Тогда уравнение имеет вид: 100t² - 100t + 9 = 0.
Ищем дискриминант:
D=(-100)^2-4*100*9=10000-4*100*9=10000-400*9=10000-3600=6400;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√6400-(-100))/(2*100)=(80-(-100))/(2*100)=(80+100)/(2*100)=180/(2*100)=180/200=0,9;
t_2=(-√6400-(-100))/(2*100)=(-80-(-100))/(2*100)=(-80+100)/(2*100)=20/(2*100)=20/200=0,1.
Обратная замена: cos(α) = ±√t.
cos(α1,2) = ±√0,9 ≈ ±0,94868.
cos(α3,4) = ±√0,1 ≈ ±0,31623.
Данным косинусам соответствуют углы:
(α1,2) = 18,43495 и 161,5651 градусов,
(α3,4) = 71,5651 и 108,43495 градусов.
По заданию угол должен быть в промежутке (90° < α < 135°).
ответ: cos α = -√0,1 ≈ -0,31623.