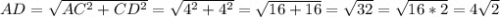Найдите сторону AD с подробным решением
Другие вопросы по теме Геометрия
Популярные вопросы
- Use phrases to complete the sentences...
1 - Автомобиль кері айналу кезінде радиусы 5 м жарты шеңбер доғасын сызады...
3 - надо, нужно ответить на вопросы ...
3 - НУЖНА Из чисел 124, 131, 146, 150, 175, 200, 208, 215, 260 выпишите...
2 - К данным наречиям подберите и запишите антонимы вниз-... Вперёд-......
1 - Найди наибольшый общий делитель чисел:16и24,10и15,14,21и49...
2 - Кому принадлежит цитата: «То, что нас не убивает, делает нас сильнее»?...
2 - Как сделать синтаксический разбор предложения Погода -состоянияатмосферы,воздуха...
1 - Жазылым Сөйлемдеғі көп нуктенің орнына тиісті қойып жаз...
2 - Ертедегі адамдар қандай кәсіптермен айналысты? 5сынып...
2
Объяснение:
В прямоугольном треугольнике ABC против угла в 30° ( ∠CAB ) лежит катет ( BC = 2 ), равный половине гипотенузы ( AC ), поэтому AC = 2 * BC = 2 * 2 = 4.
В прямоугольном треугольнике ACD ∠CAD = 90° - 45° = 45°, следовательно треугольник ACD - равнобедренный, и AC = CD = 4. По теореме Пифагора