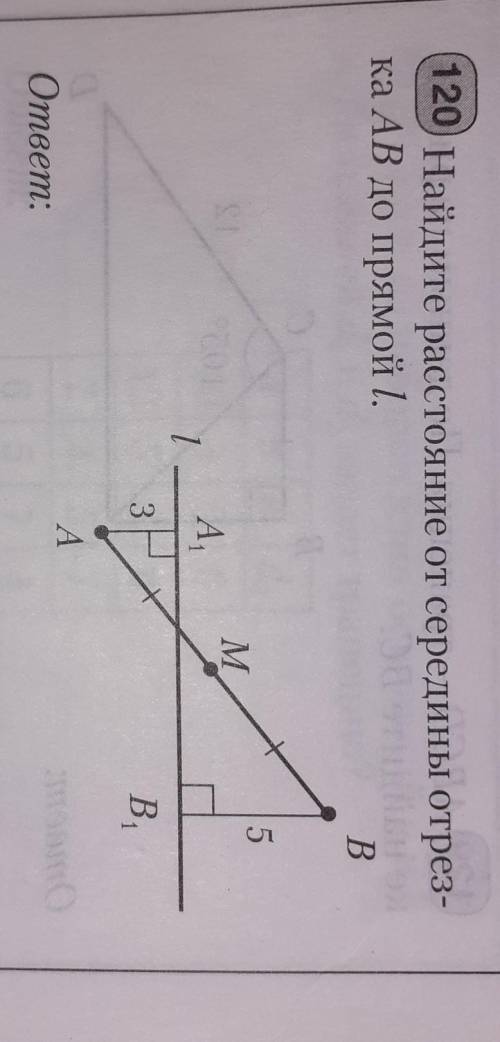
Найдите расстояние от середины отрезка AB до прямой L​

1 см

Объяснение:

Хорошо, давайте рассмотрим эту задачу.

Для начала, нужно понять, что такое середина отрезка. Середина отрезка - это точка, которая находится на равном удалении от двух концов отрезка. В данном случае, наш отрезок AB имеет две конечные точки A и B.

Чтобы найти середину отрезка AB, мы можем использовать формулу для нахождения среднего значения двух чисел. Для этого нужно сложить координаты точек A и B по каждой оси (x и y) и разделить на 2. Таким образом, мы найдем среднюю точку отрезка AB.

Для точки A координаты равны x = -4 и y = -2.
Для точки B координаты равны x = 2 и y = 2.

Теперь применим формулу и найдем координаты середины отрезка AB:
Средняя точка по оси x: (x_A + x_B) / 2 = (-4 + 2) / 2 = -2 / 2 = -1.
Средняя точка по оси y: (y_A + y_B) / 2 = (-2 + 2) / 2 = 0 / 2 = 0.

Таким образом, середина отрезка AB имеет координаты (-1, 0).

Теперь нужно найти расстояние от середины отрезка AB до прямой L. Для этого мы будем использовать формулу для нахождения расстояния от точки до прямой.

Прямая L задана в каноническом виде Ax + By + C = 0, где A, B и C - коэффициенты прямой, которые можно найти по заданным точкам.

Для заданных точек (1, 1) и (2, -3) приведем уравнение прямой L к каноническому виду. Для этого мы можем использовать формулу для нахождения коэффициентов прямой: A = y2 - y1, B = x1 - x2, C = x2y1 - x1y2.

A = (-3 - 1) = -4.
B = (2 - 1) = 1.
C = (2 * 1) - (1 * -3) = 2 + 3 = 5.

Таким образом, уравнение прямой L: -4x + y + 5 = 0.

Теперь мы можем применить формулу для нахождения расстояния от точки до прямой: d = |Ax + By + C| / √(A^2 + B^2).

Подставим координаты середины отрезка AB в формулу:
d = |-4(-1) + 0(1) + 5| / √((-4)^2 + 1^2).
d = |4 + 5| / √(16 + 1).
d = |9| / √17.
d = 9 / √17.

Таким образом, расстояние от середины отрезка AB до прямой L равно 9 / √17.