Найдите площадь равнобокой трапеции с основаниями 20 и 60 см и боковой стороной 25.

Площадь трапеции S = (b+d)*h/2

Высоту найдем из тр-ка  h = √a²-[(60-20)/2]²=√25²-20²= 15 cм

S = (60+20)*15/2 = 600 cм²

S=h(a+b)/2 (площадь трапеции равна полусумме оснований, умноженной на высоту)

Проведём высоту h. Она поделит большее основание на две части по 40 и 20 см и сама является катетом в треугольнике, где гипотенузой будет боковая сторона трапеции (25 см), а вторым катетом - часть основания (20 см). По теореме Пифагора находим высоту трапеции: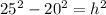 . Высота равна 15.

S=600 (см кв.)

ответ: 600.