Найдите площадь прямоугольной трапеции,большая боковая сторона которого 6√2 см,острый угол 45° и меньшее основание 4 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Придумайте рассказ по истории Рассказ от лица египетского пехотинца...
3 - Мәтін бойынша жеке сөздер, бірге, бөлек және дефис арқылы жазылатын...
1 - Найдите сумму простых делителей числа 42. А) 12; В) 5; C) 10;...
2 - Сколько будет: 15*3:9+361-954:3...
2 - При каком значение а. 24 - а меньше, чем а- 18,на 2? ...
3 - Кому з персонажив балади свитязь належать ци слова поки мужи...
2 - Архивтеру программаларын көрсет комектесндерщ...
1 - Экипаж сөзіне дыбыстық талдау ...
2 - Найти половозрастную пирамиду России и Нижегородской области...
1 - Укажите глагол, от которого образуется существительное с суффиксом...
2
Опустим высоту CH на основание AD
ΔCHD - прямоугольный и ∠CDH = 45° ⇒ и ∠DCH = 45° и он равнобедренный. Найдем:
Найдем площадь трапеции:
Здравствуй!
ΔСРД: ∠Д=45° ⇒ ∠С=45° ⇒ ΔСРД - равнобедренный и прямоугольный. Найдем стороны СР=РД по теореме Пифагора: пусть СР=РД=х см
СР=РД=6 см
ВС=АР=4 см
Sтрапеции=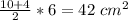
ответ: 42 см²
Удачи в учебе!