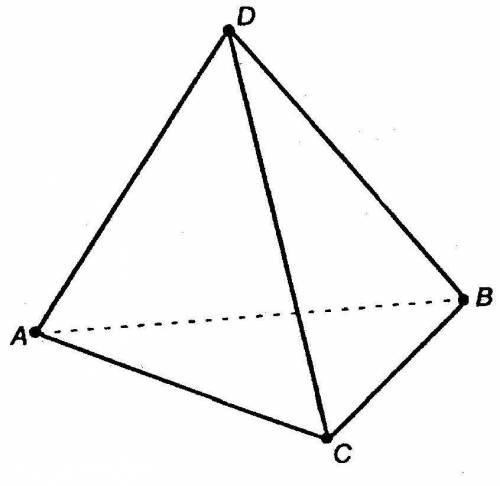
Найдите площадь сечения тетраэдра abcd, все ребра которого равны 1, плоскостью, проходящей через середины ребер AB, BC и CD (рис.)

Добрый день!

Чтобы решить эту задачу, нужно использовать знания о геометрических фигурах, плоскостях и симметрии.

Давай разберем задачу пошагово:

Шаг 1: Вспомним, что такое тетраэдр. Тетраэдр - это геометрическое тело, у которого есть четыре треугольных грани и четыре вершины.

Шаг 2: Обратим внимание на то, что в задаче указано, что все ребра тетраэдра равны 1 единице. Это значит, что все стороны треугольных граней тетраэдра тоже равны 1.

Шаг 3: Плоскость, которая задает сечение, проходит через середины ребер AB, BC и CD. Для того чтобы найти площадь этого сечения, нам понадобится найти подобные треугольники.

Шаг 4: Рассмотрим треугольники ABC и ABD. Они являются равнобедренными треугольниками, так как все стороны их равны 1. Вершина A разделена плоскостью на две отрезки AX и AY, причем AX равен половине длины AB, а AY - половине длины AD.

Шаг 5: Таким образом, мы можем сказать, что AX = 0.5 и AY = 0.5.

Шаг 6: Поскольку треугольники ABC и ABD равнобедренные, мы можем утверждать, что AX и AY являются высотами этих треугольников.

Шаг 7: Рассмотрим треугольники ABC и ACB. Заметим, что эти треугольники подобны друг другу по теореме об угловых отношениях в треугольнике. Это значит, что соответствующие стороны этих треугольников также относятся как их высоты.

Шаг 8: Пусть h1 и h2 - высоты треугольников ABC и ACB соответственно. Тогда справедливо следующее соотношение: AX / AY = h1 / h2.

Шаг 9: Подставим значения AX = 0.5 и AY = 0.5 в это соотношение и получим следующее уравнение: 0.5 / 0.5 = h1 / h2.

Шаг 10: Упростим уравнение: 1 = h1 / h2.

Шаг 11: Заметим, что треугольник ABC можно разделить на два равнобедренных треугольника ABC и ABD. Это значит, что площадь сечения плоскостью, которая проходит через середины ребер AB, BC и CD, будет равна сумме площадей этих двух равнобедренных треугольников.

Шаг 12: Пусть S1 и S2 - площади треугольников ABC и ABD соответственно. Тогда площадь сечения тетраэдра равна S1 + S2.

Шаг 13: Площади равнобедренных треугольников можно вычислить, используя формулу площади треугольника S = (1/2) * a * h, где a - длина основания, h - высота.

Шаг 14: Для треугольника ABC длины основания a1 = 1, а высоту h1 мы уже нашли на шаге 10: h1 = h2.

Шаг 15: Подставим значения a1 и h1 в формулу площади треугольника и найдем площадь S1.

Шаг 16: Для треугольника ABD длины основания a2 = 1, а высоту h2 мы уже нашли на шаге 10: h2 = h1.

Шаг 17: Подставим значения a2 и h2 в формулу площади треугольника и найдем площадь S2.

Шаг 18: Просуммируем найденные площади S1 и S2, чтобы получить итоговую площадь сечения тетраэдра.

Таким образом, площадь сечения тетраэдра abcd, все ребра которого равны 1, плоскостью, проходящей через середины ребер AB, BC и CD, равна сумме площадей треугольников ABC и ABD, где каждое основание треугольника равно 1, а высота равна высоте плоскости.

Ответ:
Площадь сечения тетраэдра равна S1 + S2, где S1 - площадь треугольника ABC, а S2 - площадь треугольника ABD. Каждая из этих площадей равна (1/2) * 1 * h, где h - высота плоскости.