Найдите ординату точки, ближайшей к точке А(-1:0) и лежащей на кривой y=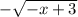 $-\sqrt{-x+3}$

Ответы

долма1 15.10.2020 16:00

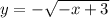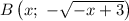Выберем на кривой $y=-\sqrt{-x+3}$ некоторую точку $B\left(x;\ -\sqrt{-x+3}\right)$ .

Найдем расстояние АВ:

$AB=\sqrt{\left(x-(-1)\right)^2+\left(-\sqrt{-x+3}-0\right)^2}$

$AB=\sqrt{\left(x+1\right)^2+\left(-\sqrt{-x+3}\right)^2}$

$AB=\sqrt{\left(x+1\right)^2+\left(-x+3\right)}$

$AB=\sqrt{x^2+2x+1-x+3}$

$AB=\sqrt{x^2+x+4}$

Так как необходимо найти ближайшую точку В к точке А, то расстояние АВ должно быть наименьшим.

Найдем, при каком значении х функция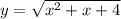 $y=\sqrt{x^2+x+4}$ принимает наименьшее значение. Так как функция корня принимает наименьшее значение при наименьшем аргументе, то это произойдет, когда аргумент 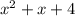x^2+x+4 примет наименьшее значение. Значит, нужно найти, при каком значении х функция 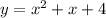y=x^2+x+4 принимает наименьшее значение. Выделим полный квадрат:

$x^2+x+4=x^2+2\cdot x\cdot0.5 +\left0.5^2-0.5^2+4=\left(x+0.5 \right)^2+3.75$

Так как квадрат любой величины не принимает отрицательных значений, то наименьшее значение достигается при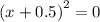 $\left(x+0.5\right)^2=0$ , то есть при x=-0.5 - графически соответствует вершине параболы.

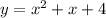При x=-0.5 функция y=x^2+x+4 принимает наименьшее значение, а значит и функция 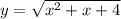$y=\sqrt{x^2+x+4}$ принимает наименьшее значение. Так как последняя функция соответствует расстоянию АВ, то именно в этом случае расстояние АВ будет наименьшим.

Найдем ординату точки В:

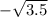
$y=-\sqrt{-x+3}=-\sqrt{-\left(-0.5\right)+3}=-\sqrt{3.5}$

ответ: $-\sqrt{3.5}$

ПОКАЗАТЬ ОТВЕТЫ

kuzma71 15.10.2020 16:00

Расстояние от точки А до точки, лежащей на кривой, должно быть наименьшим. Если в качестве точки на кривой взять точку с координатами (х;-√(-х+3)), то найдя это расстояние по формуле

√(х-х₀)²+(у-у₀)², проанализируем подкоренное выражение, и найдем координату у.

У нас А(х₀;у₀);В(х;у), значит, АВ=√((х-(-1))²+((-√(-х+3))-0)²)=

√(х²+2х+1+3-х)=√(х²+х+4) расстояние будет наименьшим, когда подкоренное выражение наименьшее. Но под корнем - квадратный трехчлен, у которого старший коэффициент равен 1, т.е. график - парабола, ветви которой направлены вверх, значит, наименьшее значение эта функция достигает в своей вершине, т.е. х=-b/2a=-1/2.

тогда у=-√((1/2)+3) =-√3.5

ответ ордината точки, ближайшей к точке А(-1;0), есть у=-√3.5

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия