Найдите объем прямой призмы, в основании которой лежит треугольник со сторонами 2 см и 6 см и углом между ними 30о, если высота призмы равна 5 см.
Если можно с рисунком
Другие вопросы по теме Геометрия
Популярные вопросы
- Для вышивания майя купила одинаковое количество мотков и шерстяных ниток .за...
1 - Списать текст, исправив ошибки всписать текст, исправив ошибки в окончаниях...
3 - Нужен 1 пример трагедии, 1 комедии и 1 драмы, с именем автора и названием самого...
3 - Аудиофайл, оцифрованный с разрядностью 16 бит и частотой дискретизации 44,1...
2 - 10 предложений про служебные части речи...
2 - Решите примеры по тригонометрии. решите уравнения, преобразовав их к квадратным,...
1 - Определите вид треугольника если два его внешних угла равны 157 и 145 градусов...
1 - Проверь верны ли равенства 478*24 больше 478*(3*9) 356*24 меньше 356*16 296*80...
3 - Осевое сечение цилиндра квадрат со стороной 6 см. найти высоту и радиус основания...
2 - Фонетический разбор слова потеряли , обсудив...
2
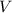 призмы
призмы 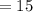 см³.
см³.
Объяснение:Обозначим данную призму буквами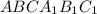 .
.
=====================================================