Найдите длину окружности, вписанной в правильный треугольник, если радиус описанной около этого треугольника окружности равен 8 см. 5-9 класс подробно 100 б
куцев
2
22.08.2019 16:20
7 
Популярные вопросы
- Как найти время, если известно масса высота и мощность ?...
1 - Какая из точек на картинке является точкой пересечения биссектрис треугольника?...
3 - Решить системы уравнений графическим методом: a б в...
2 - Составь не менее пяти слов буквы которых образуют подмножества множества...
2 - Сочинение на тему тайга наша кормилица хлопки не любит...
2 - Гаршин В. В Красный цветок, ответ на во Смерть – победа или поражение...
2 - Как вычислить интеграл (((x-2)^2)^(1/3))/x-2)^2)^(1/3))+3) в пределах...
1 - Здравствуйте с задачей(10)...
2 - Подбор лакокрасочных материалов по типу обрабатываемых поверхностей...
2 - Закончить уравнения возможных реакций.1) Na2O+N2O3=2) Co2+Fe(OH)3=3)...
3
Объяснение:
Радиус окружности, описанной около правильного треугольника со стороной а определяется по формуле :
А радиус окружности вписанной в правильный треугольник со стороной а можно найти по формуле :
Значит радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной окружности . Так как по условию
R=8 см, то r =8:2=4 см.
Найдем длину окружности по формуле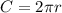
, где r -радиус окружности, вписанной в правильный треугольник, т.е. r =4 см.
Если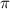
считать приближенно равным 3,14, то
С≈ 8*3,14=25,12 см.