Найдите длину гипотенузы AB прямоугольного треугольника ABC, если точка 0-центр вписанной окружности, уголOBA=30° и BC+AB=12.
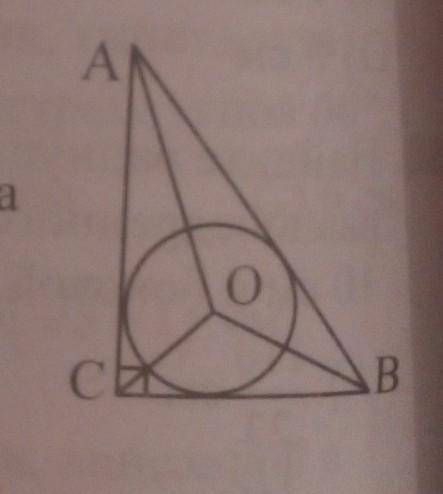
Другие вопросы по теме Геометрия
Популярные вопросы
- Объясните под влиянием каких событий в истории русского общества они появились:...
2 - Україна, Білорусь!Потрібна ваша до брати! Наведіть по 2 приклади: фонетичної,морфологічної,...
3 - Экономика-многозначное понятие. С одной стороны, это (А) занимающаясяизучением...
2 - Тема стиха Евгения Онегина глава 4...
3 - Задайте к двум видам хозяйства главный географический вопрос где? и ответьте...
3 - Укажіть кількість спільних електронних пар у молекулах етину...
1 - Нужны ещё графики этих уровнений....
3 - Выполните умножение:2/3 a×12ab2...
3 - Сочинение-рассуждение на тему какие книги я считаю драгоценными 1.Тезис (я...
3 - химия химия надеюсь видно ...
2
8
Пусть D-точка пересечения вписанной окружности и гипотенузы AB, E-точка пересечения вписанной окружности и катета BC.
В треугольнике ODB D=90°,OBD=30° =>OD=OB/2
OD=OE (оба диаметры окружности)=>OE=OB/2
В треугольнике OEC E=90°,OE=OB/2 => OBE=30°
CAB=90°-B=90°-(ABO+OBC)=90°-(30°+30°)=30°
В треугольнике ACB C=90°,CAB=30° => CB=AB/2
BC+AB=12
AB/2+AB=12
1,5AB=12
AB=12/1,5=8
Объяснение:
ΔАВС прямоугольный, ОВ - биссектриса (центр вписанной окружности лежит на пересечении биссектрис треугольника) ⇒ ∡В=30*2=60°, ∡А=90-60=30° ⇒ ВС=АВ/2 (катет прямоугольного треугольника против угла 30°);
АВ+ВС=12
АВ+АВ/2=12
3АВ=24
АВ=24/3=8 ед.