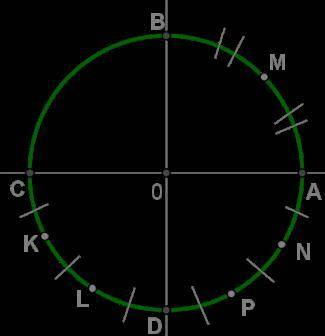
Найди все числа, которым соответствует на числовой окружности точка A . Выбери нужный вариант ответа. 3π4+2πk,k∈Z

2πk,k∈Z

π+2πk,k∈Z

π4+2πk,k∈Z

4π3+2πk,k∈Z

π2+2πk,k∈Z

−3π4+2πk,k∈Z

3π2+2πk,k∈Z

2π3+2πk,k∈Z

7π6+2πk,k∈Z

Чтобы найти все числа, которым соответствует точка A на числовой окружности, мы должны рассмотреть уравнение, которое определяет эту точку.

На числовой окружности точке A соответствует угол в радианах. Радианная мера угла на окружности равна длине дуги, поделенной на радиус окружности.

Для данной задачи длина дуги равна углу, который указан в формате десятичных долей π (например, 3π/4 или 2π/3). Чтобы найти все числа, которым соответствует точка A, мы должны найти все значения, полученные при подстановке значений k из множества целых чисел.

Давайте рассмотрим каждый вариант ответа подробнее:

1. 3π/4 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

2. 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

3. π + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

4. π/4 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

5. 4π/3 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

6. π/2 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

7. -3π/4 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

8. 3π/2 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

9. 2π/3 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

10. 7π/6 + 2πk, k ∈ Z.
Здесь мы добавляем 2πk, где k ∈ Z, чтобы учесть все возможные значения угла в рамках одной полной окружности. Ответ описывает все углы, которым соответствует точка A.

Таким образом, ответом будет:
3π/4 + 2πk, k ∈ Z;
2πk, k ∈ Z;
π + 2πk, k ∈ Z;
π/4 + 2πk, k ∈ Z;
4π/3 + 2πk, k ∈ Z;
π/2 + 2πk, k ∈ Z;
-3π/4 + 2πk, k ∈ Z;
3π/2 + 2πk, k ∈ Z;
2π/3 + 2πk, k ∈ Z;
7π/6 + 2πk, k ∈ Z.

Ученик может выбрать любой из этих вариантов ответа, так как все они являются правильными и описывают все углы, которым соответствует точка A на числовой окружности.