Найди неизвестные стороны прямоугольного треугольника ABC ( угол С= 90°), если: 1) BC=2см, cos B= 2/3. 2). AC=3см, sin B= 1/4. 3).AC=4см, ctg B=2. 4). AB= 8см, cos A=5/8. 5). AC=2см, sin A=3/5. 6). AB=6см, tg A=12/13
Другие вопросы по теме Геометрия
Популярные вопросы
- У плавильній печі для нагрівання 300кг міді від 13°C до 1083°С витратили 43кг...
1 - Природа это (история меня историчка щас сожрёт...
2 - «Промышленно-транспортная логистика» Задача...
2 - Здравствуйте! Кто разбирается в химии кто чем может! Вопросы на фото....
1 - Чому слизунів відносять до типу молюски? 7 клас...
1 - ответьте по физике (на фото)...
1 - Тупой угол равнобедренной трапеции равен 135(градусов),а высота,проведённая...
3 - Как называют время царствования Бориса Годунова?...
2 - Может ли воздух быть рабочим органом какой то технической системы? если да приведите...
3 - Розрахувати відносні молекулярні маси речовин: PbO, KCl, BaSO4....
3
Відповідь:
Пояснення:
1) AB = BC/cos B = 2/(2/3) = 3;
sin B =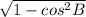 =
= 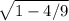 =
= 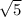 / 3;
/ 3;
AC = AB *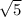 /3 = 3 *
/3 = 3 * 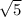 /3 =
/3 = 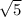 .
.
Або можна використати для обчислення третьої сторони теорему Піфагора: AC = =
=  =
= 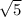 .
.
Надалі для обчислення третьої сторони використовуватиму теорему Піфагора.
2) AB = AC/sin B = 3/(1/4) = 12;
BC =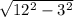 =
= 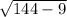 =
= 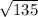 = 3
= 3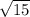 .
.
3) BC = AC*ctg B = 4*2 = 8;
AB =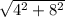 =
= 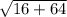 =
= 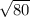 = 4
= 4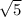 .
.
4) AC = AB*cos A = 8*(5/8) = 5;
BC = =
= 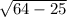 =
= 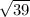 .
.
5) AB = AC/sin A = 2/(3/5) = 10/3;
BC =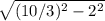 =
= 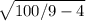 =
= 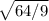 = 8/3.
= 8/3.