1. Геометрия
  2. Най­ди­те от­но­ше­ние двух

Най­ди­те от­но­ше­ние двух сто­рон тре­уголь­ни­ка, если его ме­ди­а­на, вы­хо­дя­щая из их общей вер­ши­ны, об­ра­зу­ет с этими сто­ро­на­ми углы в 30° и 90°.​

СуПерБро123 СуПерБро123    2   29.09.2020 21:55    12

Ответы
cool107 cool107  29.10.2020 21:56

1 : 2

Объяснение:


Най­ди­те от­но­ше­ние двух сто­рон тре­уголь­ни­ка, если его ме­ди­а­на, вы­хо­дя­щая из их общей в
ПОКАЗАТЬ ОТВЕТЫ
German1224 German1224  29.10.2020 21:56

Най­ди­те от­но­ше­ние двух сто­рон тре­уголь­ни­ка, если его ме­ди­а­на, вы­хо­дя­щая из их общей вер­ши­ны, об­ра­зу­ет с этими сто­ро­на­ми углы в 30° и 90°.​

Объяснение:

ΔАВС, АМ-медиана, значит ВМ=МС=х. Найдем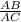   \frac{AB}{AC}  .

Для ΔАВМ по т. синусов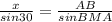     \frac{x}{sin30} =\frac{AB}{sinBMA}  .

Для ΔАСМ по т. синусов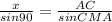     \frac{x}{sin90} =\frac{AC}{sinCMA}  .

Разделим почленно первое уравнение на второе :

   \frac{x}{sin30} :\frac{x}{sin90} =\frac{AB}{sinBMA} : \frac{AC}{sinCMA} \\  .

\frac{x}{sin30} *\frac{sin90}{x} =\frac{AB}{sinBMA} * \frac{sinCMA}{AC} \\ ,

\frac{1}{0,5} *\frac{1}{1} =\frac{AB}{AC} * \frac{sinCMA}{sinBMA} \\ ,

\frac{AB}{AC} = \frac{2*sinBMA}{sinCMA} \\ . Т.к.  sin∠BMA=sin(180-∠CMA)=sin∠CMA, то  \frac{AB}{AC} = \frac{2*sinCMA}{sinCMA} \\  

\frac{AB}{AC} = 2 .


Най­ди­те от­но­ше­ние двух сто­рон тре­уголь­ни­ка, если его ме­ди­а­на, вы­хо­дя­щая из их общей в
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
liusen liusen  27.01.2021 00:49
памагите нужна памагите нужна памагите нужна памагите ​...
Сашакозлов13лет Сашакозлов13лет  27.01.2021 00:51
памагите нужна памагите нужна памагите нужна памагите ​...
makskolisnik9ouay08 makskolisnik9ouay08  27.01.2021 00:54
памагите нужна памагите нужна памагите нужна памагите ​...
DimkaNevidimka13 DimkaNevidimka13  27.01.2021 00:54
На данной прямой находятся точки K(1;−1) и N(−1;0). Определи коэффициенты в уравнении этой прямой. (Если коэффициенты отрицательные, вводи их вместе со знаком «−»,...
tomirisestanova tomirisestanova  27.01.2021 00:59
Я ПРОСТО УМОЛЯЮ НЕ С ИНЕТА ЧТО БЫ БЫЛ РАЗВЕРНУТЫЙ ОТВЕТ С ДАНО ДОКАЗАТЬ И ДАКОЗАТЕЛЬСТВО отрезок MN и PK являются диаметрами окружности Докажите что а) угол EMP...
csioucfuo csioucfuo  27.01.2021 01:19
Задача 1. Кінці відрізка АВ, що не перетинає площину В, знаходяться на відстанях 8 см і 4 см відповідно від ціеї площини. На якій відстані від площини знаходиться...
Milkyway3000 Milkyway3000  27.01.2021 01:21
На данной прямой находятся точки K(1;−1) и N(−1;0). Определи коэффициенты в уравнении этой прямой. (Если коэффициенты отрицательные, вводи их вместе со знаком «−»,...
Megatrolll228 Megatrolll228  15.09.2019 15:50
ответь те на вопросы) 1.в каком году началась вторая мировая война? 2.когда умер юрий гагарин.в каком году? и ещё одно решительно уровнения. х+250=300 890-у=100...
sasha228111228 sasha228111228  15.09.2019 15:50
Про некий прямоугольный треугольник известно, что его площадь равна 24 и один из катетов на два меньше другого. найдите значения синусов каждого из углов треугольника....
Jack1703 Jack1703  15.09.2019 15:50
Впрямоугольном параллелепипеде abcda1b1c1d1 известны длины ребер ab=6 ad=16 aa1=8 . найдите синус угла между прямыми сс1 и ав1...

Популярные вопросы