Напиши уравнение окружности, которая проходит через точку 3 на оси Ох и через точку 7 на оси Оу, если известно, что центр находится на оси Ох. (Рассчитай в дробях, запиши не сокращая) 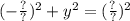
Другие вопросы по теме Геометрия
Популярные вопросы
- Составьте памятку туриста который отправляется на материк африка...
2 - Распределите обозначения времени между the present simple и the past...
1 - 1.дан одномерный массив.найти произведение элементов массива кратных...
3 - Поставьте каждое предложение в past и future simple, употребляя соответствующие...
3 - Воробей и ворона полетели с крыши в разных направлениях. ворона летала...
2 - Написати 5 речень з неологізмами.будь ласочка зараз же потрібно !...
3 - Картотека читателей библиотека хранится в ящиках в 4 ящиках лежит...
2 - Текст по . язу на тему дом будущего , не меньше 10 предложений...
1 - Придумай рассказ о выдуманном герои: например в дальнем угалке твоей...
3 - Составте слово сочетания со словами омонимами: союз,вид,обстоятельство,определение,частица....
1
ответ: (x+20/3)²+y²=(29/3)².
Объяснение:
Уравнение окружности с центром в точке O(a;b) имеет вид: (x-a)²+(y-b)²=R², где R - радиус окружности. Так как центр находится на оси ОХ, то b=0 и уравнение принимает вид: (x-a)²+y²=R². Пусть принадлежащие окружности точки А и В имеют координаты (3;0) и (0;7) соответственно. Подставляя их в уравнение окружности, приходим к системе уравнений:
(3-a)²+0²=R²
(0-a)²+7²=R²
или
a²-6*a+9=R²
a²+49=R²
Приравнивая эти уравнения, получаем уравнение -6*a=40, откуда a=-20/3. Тогда R²=841/9=(29/3)² и уравнение окружности принимает вид: (x+20/3)²+y²=(29/3)².