надо геометрия 7 класс хеелп

ответ:1)

угол DBA = 70 градусов так как в р/б треугольнике угля при оснавании равны.

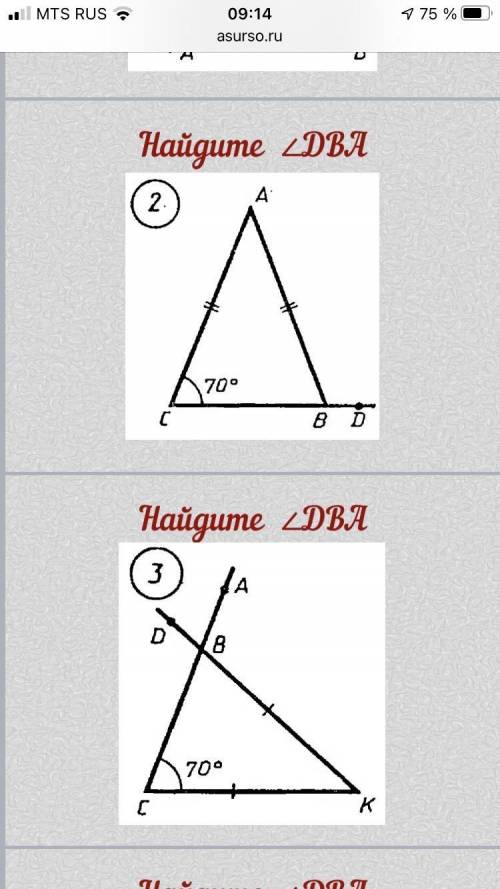
2)

угол DBA = 110 градусов так как в р/б треугольнике углы при оснавании равны следовательно угол ABC = 70 градусовследовательно угол ABC и DBA смежные углы,а сумма смежных углов 180 градусов180-70=110 градусов угол DBA

3)

угол DBA = 70 градусовт.к треугольник р/б следовательно угол CBK = 70 градусовCBK = DBK = 70 градусов (т.к углв вертикальняе, а вертик. углы равны).

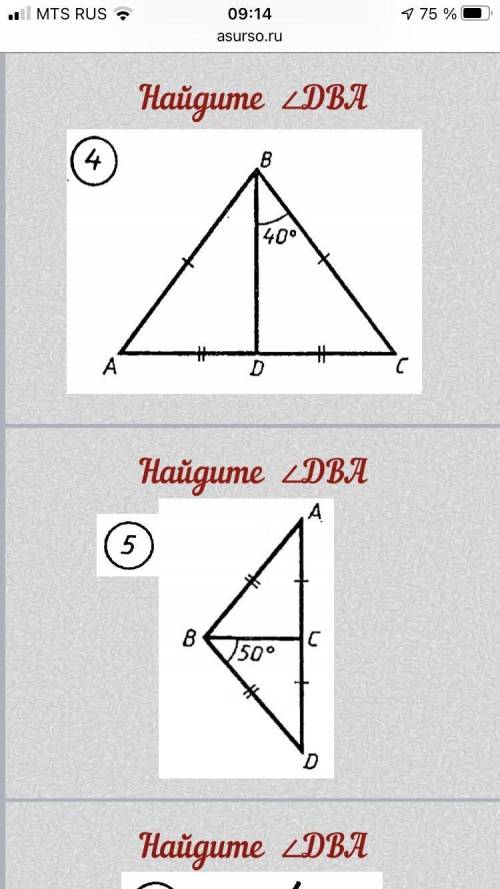
4)

треугольник р/б, медиана проведенная к основанию является и биссектрисой (биссектриса делит угол на 2 равных угла)следовательно угол DBC =DBA =40градусов

5)

треугольник р/б, медиана проведенная к основанию является и биссектрисой (биссектриса делит угол на 2 равных угла)следовательно угол 50*2 = 100 градусов угол DBA

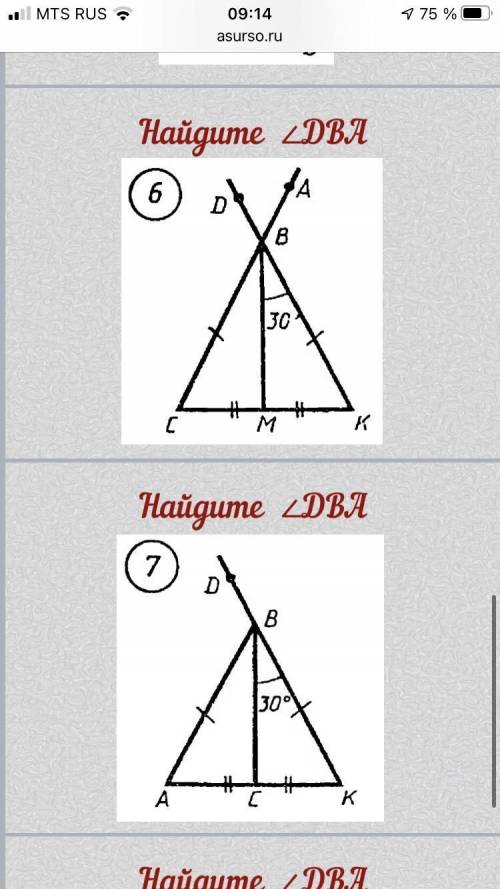
6)

треугольник р/б, медиана проведенная к основанию является и биссектрисой (биссектриса делит угол на 2 равных угла)следовательно 30×2=60 градусов угол CBKCBK=DBA=60 градусов(т.к углы вертикальные,а в вертикальные углы равны.)

7)

треугольник р/б, медиана проведенная к основанию является и биссектрисой (биссектриса делит угол на 2 равных угла)30×2=60 градусов угол ABKуглы DBA и ABK смежные, а сумма смежных углов 180 градусовследовательно 180 - 60 = 120 градусов угол DBA

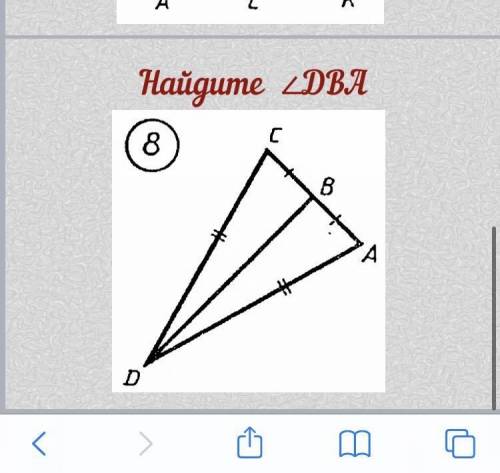
8)

сссррр

Добрый день! Рассмотрим вместе данный геометрический пример.

На данной картинке показаны две фигуры: прямоугольник ABCD и треугольник EFG. Нам нужно вычислить площадь фигуры, образованной их объединением.

1. Площадь прямоугольника ABCD:
Для этого нужно умножить длину одной из сторон на длину другой стороны. Исходя из картинки, сторона AB равна 10 единицам, а сторона BC - 8 единицам. Следовательно, площадь прямоугольника ABCD равна 10 * 8 = 80 единицам.

2. Площадь треугольника EFG:
Для нахождения площади треугольника, нужно умножить половину основания на высоту. Основание треугольника — сторона EF, а высота — отрезок, опущенный из вершины G на основание EF. Исходя из картинки, основание EF равно 12 единицам. Нам нужно найти высоту треугольника G, для этого воспользуемся теоремой Пифагора.

a^2 + b^2 = c^2, где a и b - катеты прямоугольного треугольника, а c - гипотенуза.
В нашем случае катет a = 8 (сторона BC) и c = 10 (сторона AB).
Подставляем значения в формулу и находим значение катета b:
8^2 + b^2 = 10^2 --> 64 + b^2 = 100 --> b^2 = 100 - 64 --> b^2 = 36 --> b = 6.

Теперь, когда у нас известны все три стороны треугольника EFG - EF, EG и FG - мы можем воспользоваться формулой для вычисления площади треугольника:
S = (1/2) * EF * EG
В нашем случае S = (1/2) * 12 * 6 = 36 единиц.

3. Площадь фигуры, образованной объединением прямоугольника ABCD и треугольника EFG:
Чтобы найти площадь образованной фигуры, нужно сложить площади прямоугольника и треугольника:
S общая = S прямоугольника + S треугольника = 80 + 36 = 116 единиц.

Таким образом, площадь фигуры, образованной объединением прямоугольника ABCD и треугольника EFG, составляет 116 единиц.