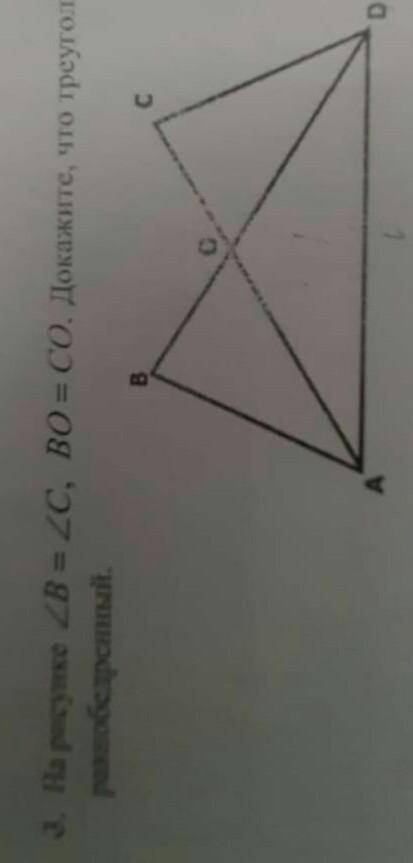
На рисунке <В=<С , ВО=СО докажите что треугольник А OD равнобедренный

Давайте рассмотрим рисунок и решим эту задачу.

Дано, что угол В равен углу С, и отрезок ВО равен отрезку СО. Мы хотим доказать, что треугольник АОД является равнобедренным.

Для доказательства равнобедренности, нам нужно показать, что две стороны треугольника равны. В данном случае, это сторона АО и сторона OD.

Шаг 1: Обратимся к предоставленному рисунку. У нас есть отрезок ВО, равный отрезку СО. Допустим, что ВО=СО=x.

Шаг 2: Рассмотрим треугольник АВО. В нем угол ВОА это угол СОА, потому что В равен С. Значит, сторона АО равна стороне АО (так как это одна и та же сторона).

Шаг 3: Рассмотрим треугольник АOD. В нем две стороны АО и OD равны, так как мы доказали это в предыдущем шаге.

Шаг 4: По определению равнобедренного треугольника, равнобедренный треугольник имеет две равные стороны. Исходя из вышеизложенного, в треугольнике АОД стороны АО и OD равны, что означает, что треугольник АОД является равнобедренным.

Таким образом, мы доказали, что треугольник АОД равнобедренный.

Надеюсь, этот ответ максимально подробный и понятный для школьника. Если у вас возникнут еще вопросы, пожалуйста, сообщите мне.