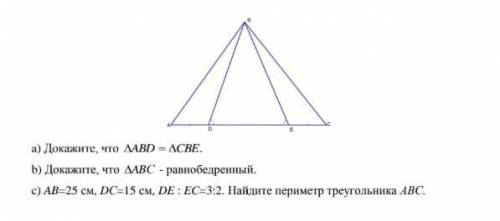
На рисунке AD=EC,<BDC=<BEA а) Докажите, что AABD - АСВЕ.
b) Докажите, что ДАВС - равнобедренный.
c) AB=25 см, DC-15 см, DE:EC-3:2. Найдите периметр треугольника ABC.​

a) Для доказательства равенства треугольников AABD и АСВЕ нужно проверить, что их соответствующие стороны и углы равны.

1. Найдем соответствующие стороны треугольников AABD и АСВЕ:
Так как на рисунке AD=EC, то сторона AD равна стороне EC.
Также на рисунке AB=BE, то сторона AB равна стороне BE.

2. Теперь найдем соответствующие углы треугольников AABD и АСВЕ:
Из условия задачи известно, что
Таким образом, мы доказали, что треугольники AABD и АСВЕ равны (по соответственности сторон и углов).

b) Для доказательства, что треугольник ДАВС - равнобедренный, нужно проверить, что две его стороны равны.

1. По условию задачи, на рисунке AD=EC и AB=BE.

2. Также из пункта a) мы уже знаем, что треугольник AABD и АСВЕ равны, поэтому сторона AB равна стороне AE.

Исходя из этих равенств, можно сделать вывод, что сторона AD равна стороне AS, и треугольник ДАВС является равнобедренным.

c) Для нахождения периметра треугольника ABC, нам не хватает информации о стороне BC. Однако, у нас есть соотношение DE:EC = 3:2.

Зная, что AD=EC, можно предположить, что DE=3x и EC=2x. Тогда, AB=BE=5x (так как AB=25 см согласно условию).

Теперь можем выразить BC через x: BC = AB - AC = 5x - 2x = 3x.

Теперь можем найти значение x, используя данное соотношение:

DE:EC = 3:2 = 3x / 2x = 3/2.

Умножим обе части на 2, чтобы избавиться от дроби:

3x = 2 * 3/2 * x = 3*x.

Теперь можем решить уравнение:

3x = 3,

x = 1.

Таким образом, мы нашли, что x = 1.

Теперь можем найти значение стороны BC:

BC = 3x = 3*1 = 3 см.

И, окончательно, можем найти периметр треугольника ABC:

Периметр треугольника ABC = AB + BC + CA = 25 + 3 + 15 = 43 см.