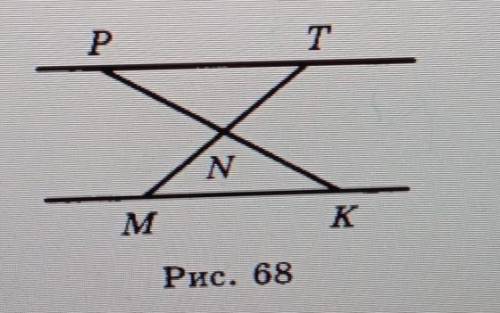
На рисунке 68 точка N- середина отрезков РК и МТ. Докажите, что прямые РТ и МК параллельны.

Чтобы доказать, что прямые РТ и МК параллельны, нам нужно использовать свойства и теоремы о параллельных прямых и серединах отрезков.

Дано: на рисунке 68 точка N является серединой отрезка РК и отрезка МТ.

Доказательство:
1. Обратимся к свойству середины отрезка: если точка является серединой отрезка, то это означает, что она делит отрезок на две равные части. В данном случае, точка N делит отрезок РК на две равные части, а также отрезок МТ на две равные части.
- Поэтому, РН = NK и NТ = TM.

2. Далее воспользуемся свойством, которое гласит: "Если две пары соответственных сторон в двух треугольниках равны, то эти треугольники подобны".
- В нашем случае, в треугольнике NРК и треугольнике NМТ стороны, соответствующие друг другу, равны между собой: РН = NK и NТ = TM.
- Поэтому, по свойству, треугольники NРК и NМТ подобны.

3. Теперь обратимся к свойству подобных треугольников: "Если две пары противоположных сторон подобных треугольников параллельны, то все стороны подобных треугольников параллельны".
- В нашем случае, прямые РК и МТ являются противоположными сторонами треугольников NРК и NМТ, которые мы только что установили как подобные.
- Поэтому, по указанному свойству, прямые РТ и МК также параллельны.

Таким образом, мы доказали, что прямые РТ и МК параллельны, основываясь на свойствах и теоремах о параллельных прямых и серединах отрезков, а также на подобии треугольников.