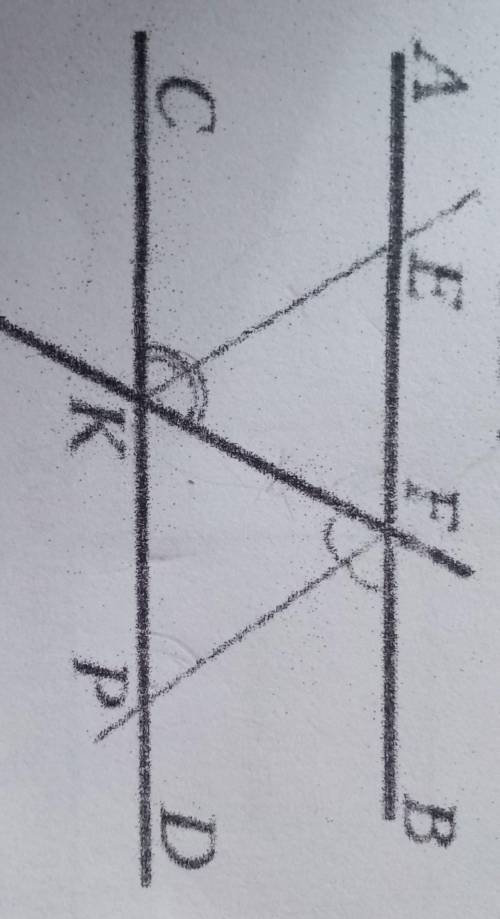
На рисунке 181 биссектриса угла CKF пересекает прямую AB в точке E, a биссектриса угла KFB пересекает прямую CD в точке P. Докажите, что если EF=FK, то EF=KP. ​

Для начала докажем, что треугольники KFE и KPF подобны. В треугольнике KFE угол KEF является внутренним углом треугольника и равен половине угла K, так как биссектриса делит угол на два равных угла. Также, угол KFE внутренний угол треугольника, так как он лежит внутри треугольника. Поэтому, угол KFE тоже равен половине угла K. Аналогично, в треугольнике KPF угол KPF равен половине угла K (по свойству биссектрисы) и угол KFP также равен половине угла K. Таким образом, у треугольников KFE и KPF совпадают два угла, что означает, что эти треугольники подобны по признаку двух углов. Теперь, чтобы доказать, что EF=KP, нам осталось показать, что соответствующие стороны подобных треугольников пропорциональны. Если мы обратим внимание на соответствующие стороны, то увидим, что сторона EF является продолжением стороны FK, а сторона KP является продолжением стороны PF. Мы знаем из условия, что EF=FK, значит, сторона EF соответствует стороне FK на изображении. А по свойству подобных треугольников, соответствующие стороны должны быть пропорциональны. То есть, EF/FK = KP/PF. Теперь мы можем воспользоваться перестановочным свойством равенства и получить, что EF/KP = FK/PF. Затем, мы можем умножить обе части этих равенств на PF и получить EF * PF = KP * FK. Но мы знаем, что EF = FK, поэтому мы можем заменить FK на EF в этом равенстве: EF * PF = KP * EF. А затем мы можем сократить обе части равенства на EF и получить PF = KP. Таким образом, мы доказали, что если EF=FK, то EF=KP.