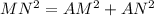На отрезке MN выбрана точка С так, что МС = 40, СN =10. Постройте окружность с центром в точке М, проходящую через точку С. Проведите к этой окружности касательную NA, где А - точка касания. Найдите длину отрезка NA.
1) 20
2) 25
3) 30
Другие вопросы по теме Геометрия
Популярные вопросы
- Природные зоны австралии, обитатели этих зон и растения. буду . если у кого то...
3 - Меньшее основание прямоугольной трапеции равно a см, а остр угол -30 градусам,...
3 - Найти предел функции lim x- +∞(x^2+2^x)/(3*x^3-1)...
2 - Где в россии расположена зона полупустынь и пустынь? (кратко)...
1 - Нужно решить 3,8+14= 26,7+3= 0,58+0,2= 6,05+05= 3,57+0,03= 0,45+0,55= 8,9-5,4=...
1 - Проэкт по языку здоровый образ жизни 5 класс...
1 - Гидроксид алюминия является амфотерным, потому что...
2 - Как вы оцениваете характер второй мировой войны, что вы можете сказать о целях...
1 - Расстояние между двумя параллельными плоскостями 3см. отношение проекций двух...
3 - 1. чему равна сумма квадратов корней уравнения x^2(x+1)(x+1)=0? 2. при каких значениях...
2
30
Объяснение:
Проведем отрезок МА, где А - точка касания окружности и касательной.
МА перпендикулярен к касательной (по свойству касательной), т.е. угол между МА и касательной AN равен 90°.
Следовательно, треугольник AMN - прямоугольный.
MA=MN=75 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По теореме Пифагора: