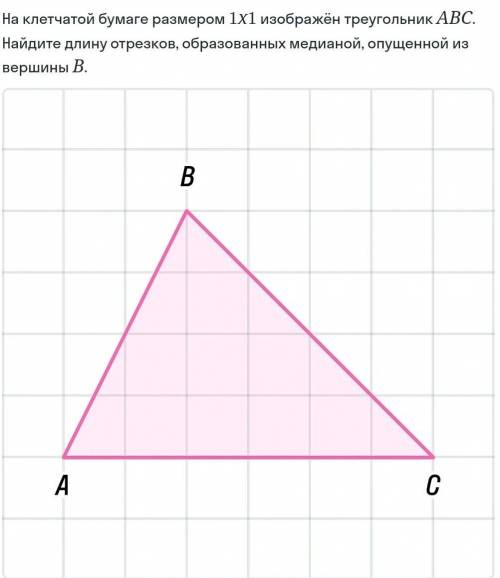
На клетчатой бумаге размером 1X1 изображён треугольник АВС. Найдите длину отрезков, образованных медианой, опущенной из
вершины В.​

4 клетки

Объяснение:

Медиана, проведенная из вершины B показана красной линией на рисунке ниже.

Ну и уже там видно что Медиана равна 4 клеткам.

Для начала, давайте вспомним, что такое медиана треугольника. Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае, мы ищем длину медианы, опущенной из вершины В.

Чтобы решить эту задачу, нам нужно понять, как выглядит треугольник.

Первое, что мы видим, что у треугольника есть вершины A, B и C. Из условия задачи мы знаем, что на клетчатой бумаге размером 1x1 изображен треугольник, значит, каждая сторона треугольника покрывает одну клетку.

Давайте обозначим точки M, N и P - середины сторон треугольника AB, BC и AC соответственно.

Теперь, давайте посмотрим на сторону AB треугольника. Мы видим, что медиана, опущенная из вершины В, соединяет вершину В с серединой стороны AB, то есть точкой M. Таким образом, мы ищем длину отрезка BM.

Чтобы найти его длину, нам нужно знать координаты точек B и M. Для этого нам пригодится информация о клетчатой бумаге.

По условию задачи, мы знаем, что каждая клетка имеет размер 1x1. То есть, расстояние между двумя соседними клетками равно 1. Поскольку медиана, опущенная из вершины В, проходит через точку M - середину стороны AB, то расстояние между точками B и M будет равно половине длины стороны AB.

Длина стороны AB равна 4 клеткам, поэтому половина ее длины будет равна 4/2 = 2 клеткам.

Таким образом, мы получаем, что длина отрезка BM - это 2 клетки.

Ответ: Длина отрезков, образованных медианой, опущенной из вершины В, равна 2 клеткам.