Люди нужна боковое ребро правильной треугольной пирамиды, у которой боковая поверхность равна 60√3 см^2, а полная поверхность - 108√3 см^2

т.к. площадь всей поверхности равна 108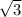,а площадь боковой поверности 60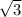,то площадь основания равна 48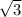,а так же равна  a^2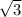/4,тогда а-длина ребра основания равна 8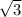

т.к. площадь боковой поверхности равна 60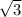,а так же ранвна Pосн*h/2,где h-апофема,,а Pосн=3a,то h=5,т.к пирамида правильноя,то боковые грани равны,и являются равнобедренными треугольниками,тогда h-медиана,тогда

b-бокове ребро найдем по теореме Пифагора b=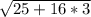=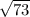см

Хорошо, для начала давайте разберемся, что такое боковая поверхность и полная поверхность правильной треугольной пирамиды.

Боковая поверхность - это общая площадь боковых граней пирамиды. В нашем случае, боковая поверхность равна 60√3 см^2.

Полная поверхность - это площадь всех граней пирамиды, включая основание. В нашем случае, полная поверхность равна 108√3 см^2.

Теперь давайте решим задачу. Пусть a - длина стороны основания пирамиды, h - высота боковой грани пирамиды, и l - длина бокового ребра.

У правильной треугольной пирамиды у нас есть 4 боковые грани, каждая из которых является равнобедренным треугольником, у которого две стороны длиной a и третья сторона длиной l.

Теперь мы можем использовать формулы для нахождения площади поверхности пирамиды:

Площадь боковой поверхности боковой грани = (1/2) * a * h

Площадь основания пирамиды = (a^2 * √3) / 4

Теперь мы можем записать уравнения для нахождения a и h, и затем использовать эти значения для нахождения l.

1) Площадь боковой поверхности = (1/2) * a * h
Из условия задачи мы знаем, что площадь боковой поверхности равна 60√3 см^2, поэтому 60√3 = (1/2) * a * h

2) Площадь основания = (a^2 * √3) / 4
Из условия задачи мы знаем, что полная поверхность равна 108√3 см^2, поэтому 108√3 = (a^2 * √3) / 4

Теперь давайте решим эти уравнения.

1) 60√3 = (1/2) * a * h
У нас нет информации о значении h, поэтому нам не удастся найти точные значения для a или h без дополнительной информации.

2) 108√3 = (a^2 * √3) / 4
Если мы домножим обе части уравнения на 4, мы получим:
432√3 = a^2 * √3
Делая квадратный корень от обеих частей уравнения, мы получим:
a = √432
a = 12√3

Теперь давайте найдем длину бокового ребра пирамиды, l, используя теорему Пифагора:
l^2 = a^2 + h^2

Мы уже знаем значение a = 12√3, и нам необходимо найти значение h. У нас нет непосредственной информации о h, однако мы можем использовать площадь основания пирамиды, чтобы решить это.

Площадь основания пирамиды = (a^2 * √3) / 4
108√3 = (12√3)^2 * √3 / 4
108√3 = (144 * 3) * √3 / 4
108√3 = 432√3 / 4
Перемножим обе части уравнения на 4:
432√3 = 432√3

Итак, мы получили равенство, которое означает, что мы ошиблись в предположении о значении a = 12√3. Это значит, что мы не можем найти точное значение длины бокового ребра пирамиды без дополнительной информации.

В заключении, мне жаль, но без дополнительных данных мы не можем ответить на вопрос о длине бокового ребра правильной треугольной пирамиды.