Квадрат 10х10 разрезали на прямоугольники по линиям сетки площади которых различны и выражаются натуральными числами. какое наибольшее число прямоугольников получиться ? пример
Ответы
Площадь квадрата равна 100. Если представить 100 в виде суммы натуральных чисел, то число слагаемых будет наибольшим, если разность между числами равна одному. Возьмем прямоугольники площади 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Их суммарная площадь равна 55. Значит, сумма площадей остальных прямоугольников равна 45. Заметим, что если площадь прямоугольника больше 10, то она не может быть простым числом, иначе такой прямоугольник имеет сторону больше 10 и не помещается в квадрат 10×10 . Составными числами больше десяти являются числа 12, 14, 15, 16, 18, 19,… Любые четыре из них в сумме дают число больше 45. Сумму, равную 45, дают, например, такие тричисла: 12,15,18 или 14,15,16. Получаем, что число прямоугольников меньше или равно 13. Пример возможного расположения для 13 прямоугольников приведен на рисунке.
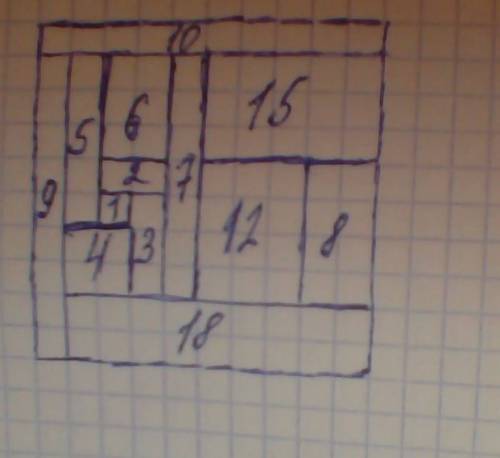
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Причина создания жети-жархы и основные его положения...
2 - Докажите, что театр лучший вид искусства. красноречиво и чётко...
2 - Берілген суреттерді тірек сөздердін көмегімен сипаттаңыз (әр білім 2 минуты)...
3 - Чем заканчивается роман пастернака доктор живаго...
1 - Зробіть розбір речення: вже на річках дитячий галас вщух, холонуть дні, і все...
1 - Точка около 10 см в правом треугольнике, а стены √73 см. найти расстояние от...
2 - 2-й класс кузовлёв 2 часть рабочая тетрадь стр.95 №2...
1 - 9класс, контрольная итоговая ! напишите уравнения реакций, с которых можно осуществить...
2 - Поиогите зделать дз по страница 126 номер 1 2 3 5 класс...
1 - Про треугольник abc известно, что ab=10, ac=16, bc=9. на стороне bc выбрана точка...
2