КР. Диагональ боковой грани правильной треугольной призмы равна 12см² и образует с плоскостью основания угол 60°. Найдите площадь полной поверхности призмы. С РИСУНКОМ .

Ответы

lolSashalolo 15.10.2020 12:47

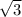
126 $\sqrt{3$

Объяснение:

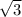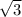
Высота призмы BB1=AB1*sin60=12* $\sqrt{3$ /2=6 $\sqrt{3$

Сторона основания AB=AB1*cos60=12*1/2=6

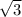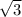
Площадь боковых сторон равна 3*6*6 $\sqrt{3$ =108 $\sqrt{3$

Площадь основний равна 2*6^2*/4=18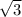 $\sqrt{3$ (Формула площади равностороннего треугольника)

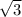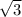
Площадь полной поверхности равна (18+108) $\sqrt{3$ =126 $\sqrt{3$

ПОКАЗАТЬ ОТВЕТЫ

Shahi95 15.10.2020 12:47

площадь полной поверхности призмы будет равна: 126√3.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Nazar07072004 20.11.2020 10:47

polikzaisheva12 07.03.2019 23:30

Найдите ошибку если угол м=76,угол к=40 и угол n=40...

azalia2003love 07.03.2019 23:30

Lol11111111000 07.03.2019 23:30

lewa0131 07.03.2019 23:30

СулеймановаНигяр 07.03.2019 23:30

Найти tg a , если sin a =3/5 cos a = 5/12...

vvvlll1 07.03.2019 23:30

ElDiablo1337 07.03.2019 23:30

vikapuzya200 07.03.2019 23:30

valeria03mailowfj4z 07.03.2019 23:30