KP||AD||BC найдите длину отрезка CP
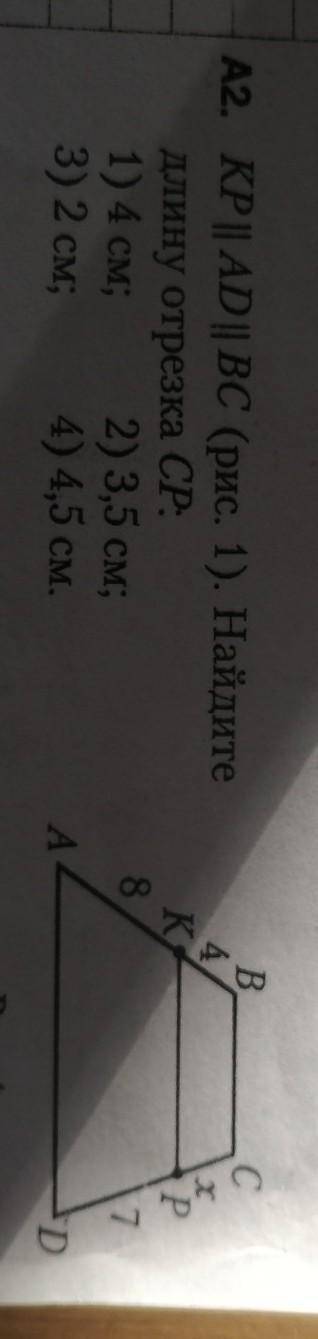
Другие вопросы по теме Геометрия
Популярные вопросы
- высота равностороннего треугольника равна 4,2см. Найдите расстояние от точки...
2 - сегодня нужен бергенге под етем...
3 - Труд Продолжи предложения, выбрав соответствующий вариант из списка.1. - Такие...
1 - помгите эссе на тему: Славянская мифология....
2 - 6. Their son___in this hospital. a)works b)begins c)starts d)lakes 7.Jim s...
3 - 7 тапсырма қазақстандағы әлемдік құндылық болып бағаланатын мұралар туралы...
1 - Терминге сәйкес келетін анықтаманы тап....
2 - Хрестоматиядан «Алып Ер Тұңға» жырын оқып, Ер Тұңғаның жасаған ерлік істерін...
2 - Берілген сөздің синонимін мәтіннен тауып жазыңыз баяғда...
3 - Выбери материалы и инструменты для работы с пластилином. Верных ответов: 2доска...
2
В данной задаче, у нас есть две пары параллельных прямых – KP||AD и KP||BC. По свойствам параллельных прямых, у нас появляются несколько равных углов:
Угол DAK равен углу A, так как они являются смежными и параллельными линиями.
Угол KPA также равен углу A, так как они являются вертикальными углами и параллельны линии AD.
Таким образом, треугольник KPA является подобным треугольнику DAK. Кроме того, треугольник KPA подобен треугольнику BCP, поскольку у них одинаковые соответственные углы: BCP равен углу C, а KPA равен углу A.
Так как треугольники KPA и DAK подобны, мы можем использовать соответствующие стороны треугольников для поиска длины стороны KP. Соотношение соответствующих сторон для подобных треугольников можно записать как:
KP/DAK = PA/AK
Мы знаем, что сторона DAK равна 9 см (значение дано на рисунке), а сторона PA равна 3 см (значение также дано на рисунке). Нам нужно найти длину стороны KP.
Таким образом, уравнение будет выглядеть следующим образом:
KP/9 = 3/AK
Мы также знаем, что треугольник KPA и треугольник BCP подобны. Поэтому мы можем записать еще одно подобное уравнение:
KP/BCP = PA/PC
Из предыдущих вычислений мы знаем, что сторона PA равна 3 см, а сторона BCP равна 6 см (значение дано на рисунке). Мы также не знаем длину стороны KP и сторону PC.
Поэтому уравнение будет выглядеть следующим образом:
KP/6 = 3/PC
Теперь у нас есть два уравнения с двумя неизвестными (KP и PC). Мы можем использовать метод подстановки или решить систему уравнений, чтобы найти значение KP.
Сначала мы можем изолировать KP в первом уравнении:
KP = 3/DAK * AK
KP = 3/9 * AK
KP = AK/3
Затем мы можем подставить это значение KP во второе уравнение:
AK/3/6 = 3/PC
AK/18 = 3/PC
PC = 18/3 * AK
PC = 6AK
Теперь у нас есть значение PC в терминах AK. Однако, мы также наблюдаем, что треугольник KPA и треугольник ABC подобны по теореме Пифагора, поскольку имеют одинаковые углы и соответствующие прямые углы.
Мы знаем, что сторона AK равна 5 см (значение дано на рисунке). Также, мы знаем, что сторона AC равна 13 см (значение дано на рисунке).
Теперь мы можем найти длину стороны KP, используя ранее найденное значение PC и сторону AK:
KP = AK/3
KP = 5/3 см
Таким образом, длина отрезка CP равна 5/3 см.