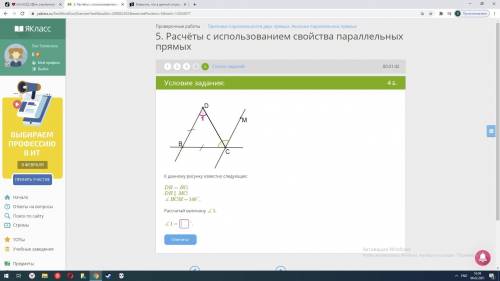
К данному рисунку известно следующее: DB=BC;
DB∥MC;
∡BCM = 148°.

Рассчитай величину ∡1.

∡1 =

По условию ВD║МС, значит внешний ∠В=∠ВСМ=142°, тогда по свойству внешнего угла ∠1+∠ВСD=142°.

По условию BD=BC, значит ΔСBD равнобедренный и ∠1=142°/2=71°.

ответ: ∠1=71°.

74°

Объяснение:

∠1=∠DCM как внутренние накрест лежащие при BD║СМ и секущей СD

∠1=∠ВСD как углы при основании равнобедренного треугольника

∠ВСD=148:2=74°,  ∠1=74°