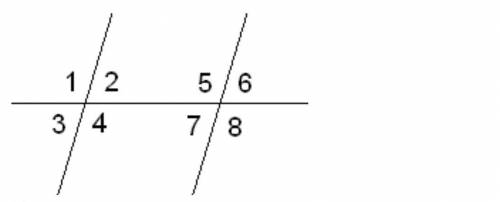
Известно, что две параллельные прямые пересекаются третьей прямой, ∢3=62°. Вычисли все углы.
∢1= °
∢2= °
∢3= °
∢4= °
∢5= °
∢6= °
∢7= °
∢8= °
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение -7(3х-8)+3(4х-5)=8...
2 - Расскажите о самостоятельных и служебных частях речи. примеры. надо,...
3 - Грузовику надо увезти 3200 кг металлолома. в первый день он увёз 45% всего груза....
2 - Вычисли периметр прямоугольника ,если его площадь равна 140 см в квадрате(больше...
2 - 118 прочитайте составте предложение по данному началу запишите их подчеркните...
1 - 675+25242+758+1325 вычислить рациональным...
3 - Как в html сделать текст справа от картинки...
3 - Вмотке 40 м провода.десятую часть всего провода израсходовали на ремонт электропроводки,а...
2 - (гончар).чем работа людей этой профессии полезна обществу ?...
1 - Решите уравнение: 1 - х +х² - х³= 5 - (х³ - х² +х)...
3
Объяснение:
главное пойми, то, что у меня списал))всегда ))
Из свойства параллельных линий, мы знаем, что когда прямые линии пересекаются третьей прямой, вертикальные углы равны друг другу. То есть ∢3 равен ∢6.
Теперь, мы также знаем, что ∢3 равен 62°, следовательно, ∢6 также равен 62°.
Также, у нас есть свойство треугольников, которое гласит, что сумма всех углов треугольника равна 180°.
Мы можем использовать это свойство для вычисления ∢7 и ∢8.
∢4, ∢5, ∢6 и ∢7 образуют треугольник. Он должен иметь сумму углов 180°. Так как мы знаем, что ∢6 = 62°, мы можем вычислить ∢7:
∢4 + ∢5 + ∢6 + ∢7 = 180°
∢7 = 180° - (∢4 + ∢5 + ∢6)
То есть, мы можем заменить ∢7 на 180° - (∢4 + ∢5 + 62°).
Теперь мы знаем, что ∢7 равно ∢8, поэтому мы можем записать:
∢8 = 180° - (∢4 + ∢5 + 62°)
Таким образом, мы получили выражения для вычисления ∢7 и ∢8. Теперь нам нужно выразить ∢1 и ∢2 через другие углы.
∢1 и ∢2 являются вертикальными углами и равны друг другу. Поэтому:
∢1 = ∢2
Теперь у нас есть все данные для вычисления всех углов. Мы можем использовать эти выражения для расчета значений углов в соответствии с заданными условиями.