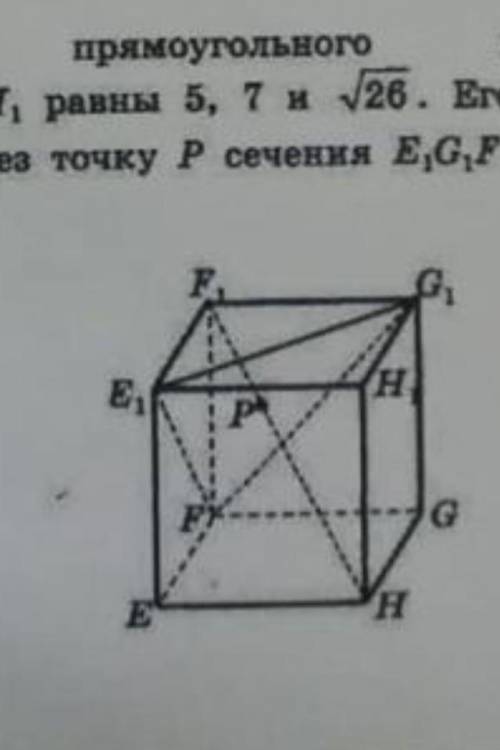
Измерения прямоугольного параллелепипеда EFGHE1F1G1H1 равны 5,7 и √26. Его диагональ HF1 проходит через точку P сечения E1G1F.Найдите длину отрезка F1P.
Другие вопросы по теме Геометрия
Популярные вопросы
- Как перевести в соответствии с международной системой единиц си, где: t-время в...
1 - Укажите множество значений функции y=3-㏒₀,₃x...
2 - Найдите значение cos a, если известно, что sin a=1/5 и a=2 четверти...
1 - Найдите значение производной функции f(x)=x^3 - 3x в точке = 2...
3 - Вычислите значение выражения: умножить на 3^2/3...
3 - Краткое содержание сказки марья моревна 5 6 предложений...
3 - Объясните, , подробно, как решать тригонометрические подробно, ибо я совсем ничего...
3 - Найдите точки пересечения графиков функций y=√x²+16 и y=3x-4...
2 - По информатике, арифметические выражения на языке qbasic. у старого черта в гостях...
3 - Определите норму и сумму годовой амортизации на и а, если первоначальная () стоимость...
1
У нас есть прямоугольный параллелепипед EFGHE1F1G1H1, у которого известны две измерения сторон – 5 и 7, и требуется найти длину отрезка F1P, где P – это точка пересечения диагонали HF1 с плоскостью E1G1F.
Для начала, найдем общие измерения прямоугольного параллелепипеда. Зная размеры его сторон, мы можем использовать теорему Пифагора для нахождения длины диагонали HG1.
Длина HG = √(EF^2 + EG^2)
= √(5^2 + 7^2)
= √(25 + 49)
= √74
Теперь, используя измерения EF, EG и HG1, мы можем найти отношение F1G1 к HG1.
GF1/GG1 = EF/EG
F1G1/√74 = 5/7
Далее, учитывая, что медиана F1P делит треугольник F1G1G1 на две равные части, мы можем сделать вывод, что отношение медианы F1P к отрезку F1G1 также равно 1:1.
F1P/F1G1 = 1/1
Теперь у нас есть два уравнения:
F1G1/√74 = 5/7
F1P/F1G1 = 1/1
Мы можем использовать данные уравнения для нахождения длины отрезка F1P.
Сначала, найдем длину отрезка F1G1:
F1G1 = (√74 * 5)/7
Затем, используя это значение, найдем длину отрезка F1P:
F1P = (F1G1 * 1)/1
Итак, ответом на вопрос является длина отрезка F1P.+