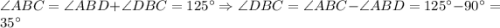Из вершины угла равного 125 во внутреннюю его область проведен луч, перпендикулярный одной из его сторон. чему равен угол, образованный данным лучаом с другой стороной угла?
Другие вопросы по теме Геометрия
Популярные вопросы
- Заполни пропуски: 7 см2= 13 дм2= 17 дм2= 32 м2= 12 га= 14 см2= 6 км2= 44 м2=...
2 - Где фразеологизмы -в детстве слушал бабушкинъ сказки.отрезной ломать хлеба...
2 - Что взять в автобус 3-4 часа езды, из еды и разных мелочей? что взять чтобы...
3 - Написать сочинение на языке с переводом про любую реку мира....
2 - Розв яжіть ситуацію. хлопці 16 та 14 років на території школи розпивали спиртні...
2 - Втреугольнике орт угол о = 90 гр, рт = 15, cos =0,8. найдите от....
1 - 30 ! с решением. 1. автомобиль движется с постоянной скоростью 65 км/ч. за какое...
1 - Уравнение касательной к графику функции y = -1 + 2x + x^2 + 2e^x в точке с абсциссой...
3 - Поставь правильно знаки 2 5 7 8 9 4=13...
1 - Эссе на тему: что такое настоящая красота...
2
1)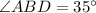 ; 2)
; 2)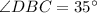
Объяснение:
Рассмотрим два решения (но при этом ответ не поменяется):
Обозначим данный угол буквами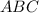 .
.
Проведём луч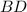 , перпендикулярный лучу
, перпендикулярный лучу 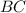 .
.
угол, образованный данными лучами с другой стороной угла -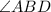 .
.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Т.е.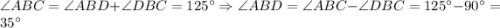
Обозначим данный угол буквами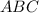 .
.
Проведём луч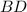 , перпендикулярный лучу
, перпендикулярный лучу 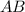 .
.
угол, образованный данными лучами с другой стороной угла -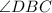 .
.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Т.е.