Из данной точки проведены к данной плоскости две равных наклонные угол между наклонной равно 60, а угол между их проекциями прямой докажите что каждая из этих наклонных образует с плоскостью угол 45
Ответы
Поскольку наклонные равны, значит и их проекции будут равны между собой. Далее, если рассмотреть треугольник, который составляют наклонные, то он правильный, поэтому если проекция наклонной равняется Х, то сторона этого треугольника будет равняться Х* 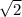 . После, если рассмотреть треугольник, который составляет наклонная и ее проекция, то мы видим, что он прямой. В нем мы знаем величину катета и гипотенузы, поэтому сейчас необходимо доказать, что этот треугольник - равнобедренный. Поскольку гипотенуза что в данном треугольнике, что в предыдущем рассмотренном равна, а так же равен один из катетов, мы делаем вывод, что второй катет так же равен (из равенства прямоугольных треугольников). Поэтому, в равнобедренном треугольнике, где угол при вершине - прямой, остальные углы равняются по 45 градусов.
. После, если рассмотреть треугольник, который составляет наклонная и ее проекция, то мы видим, что он прямой. В нем мы знаем величину катета и гипотенузы, поэтому сейчас необходимо доказать, что этот треугольник - равнобедренный. Поскольку гипотенуза что в данном треугольнике, что в предыдущем рассмотренном равна, а так же равен один из катетов, мы делаем вывод, что второй катет так же равен (из равенства прямоугольных треугольников). Поэтому, в равнобедренном треугольнике, где угол при вершине - прямой, остальные углы равняются по 45 градусов.
ПОКАЗАТЬ ОТВЕТЫ
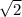 . После, если рассмотреть треугольник, который составляет наклонная и ее проекция, то мы видим, что он прямой. В нем мы знаем величину катета и гипотенузы, поэтому сейчас необходимо доказать, что этот треугольник - равнобедренный. Поскольку гипотенуза что в данном треугольнике, что в предыдущем рассмотренном равна, а так же равен один из катетов, мы делаем вывод, что второй катет так же равен (из равенства прямоугольных треугольников). Поэтому, в равнобедренном треугольнике, где угол при вершине - прямой, остальные углы равняются по 45 градусов.
. После, если рассмотреть треугольник, который составляет наклонная и ее проекция, то мы видим, что он прямой. В нем мы знаем величину катета и гипотенузы, поэтому сейчас необходимо доказать, что этот треугольник - равнобедренный. Поскольку гипотенуза что в данном треугольнике, что в предыдущем рассмотренном равна, а так же равен один из катетов, мы делаем вывод, что второй катет так же равен (из равенства прямоугольных треугольников). Поэтому, в равнобедренном треугольнике, где угол при вершине - прямой, остальные углы равняются по 45 градусов.
Другие вопросы по теме Геометрия
Популярные вопросы
- Подписать падежи которым относится данное окончание примеры имён существительных...
2 - Найдите число, 5/7 которого составляет 40...
3 - 249. велосипедист за несколько часов проехал 36 км. а) какое расстояние...
3 - Подобные члены и найдите значение многочлена при указанных значениях переменных:...
2 - Выпишите четыре числа которые кратн числу 35...
3 - Обясни решение уравнения и проверку х+6=38...
2 - 1. в каком варианте во всех словах пропущена буква и ? 1) у , в , к 2)...
3 - Что написать в графе мои яркие впечатления....
3 - Найдите площадь равнобедренной трапеции, если ее основания равны 3 см и...
1 - Отзыв по книгам дубровский и барышня крестьянка пушкин...
1