Используя данные рис.1 найдите площадь треугольника с высотой 4√3 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Work in pairs. Discuss with your partner the following: 1 What...
2 - Find pairs of words that have similar meanings. Read them. big,...
3 - Match the countries and the word combinations corresponding to...
3 - Discuss in groups of 3-4 what you know about English-speaking...
1 - Before you read the texts about English-speaking countries guess...
3 - Have you ever heard about Esperanto? Where is Esperanto spoken?...
2 - Find the pairs of words that have the same pronunciation. there,...
3 - Remember what you know about personal characteristics of people...
1 - Listen, read and act out. George meets a group of foreign participants....
3 - Read, compare and remember. 1. Have you seen the boy (who / that)...
3
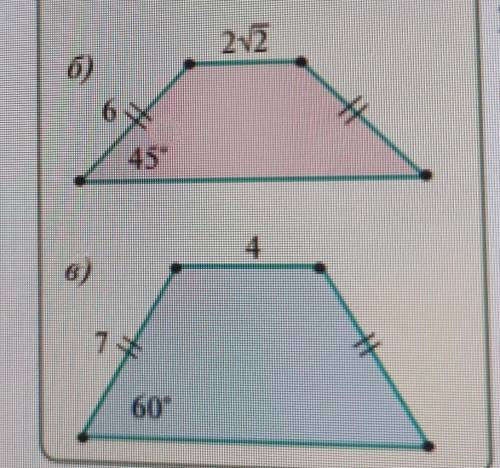
а)
∆АВМ- прямоугольный равнобедренный треугольник. Углы при основании равны 45°.
АМ=ВМ.
АМ=АВ/√2=6/√2=3√2 ед.
BM=3√2ед
МН=ВС=2√2ед
АD=2*AM+MH=2*3√2+2√2=8√2ед.
S(ABCD)=BM(ВС+АD)/2=
=3√2(2√2+8√2)/2=3√2*10√2/2=30ед²
ответ: 30ед²
б)
∆LMH- прямоугольный треугольник
LH- катет против угла <LMH=30°
LH=LM/2=7/2=3,5 ед.
LK=2*LH+MN=2*3,5+4=11ед.
По теореме Пифагора
МН=√(LM²-LH²)=√(7²-3,5²)=3,5√3 ед.
S(LMNK)=MH(MN+LK)/2=3,5√3(4+11)/2=
=3,5√3*15/2=26,25√3 ед²
ответ: 26,25√3 ед²