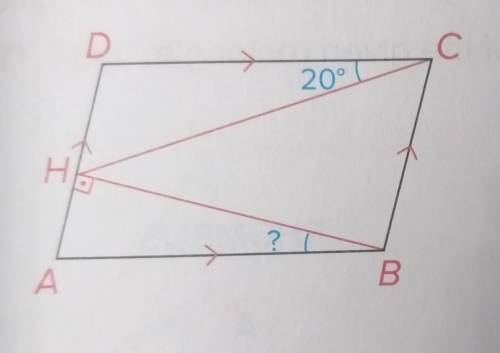
In the figure, ABCD is a parallelogram with BH AD and BH = AD. If
m(HCD) = 20° , find m(ABH). Help

Для того чтобы найти m(ABH), нам понадобится использовать свойства параллелограммов и углы, образующиеся при пересечении параллельных линий.

Из условия задачи, мы знаем, что ABCD - параллелограмм, поэтому угол ACD равен углу BDC (потому что они являются соответственными углами при пересечении параллельных линий). Также, мы знаем, что угол HCD = 20°.

Мы также знаем, что BH = AD, поэтому треугольник BAH является равнобедренным треугольником (потому что у него две равные стороны).

Теперь давайте рассмотрим угол HAB. Поскольку треугольник BAH равнобедренный, угол HAB равен углу HBA. По свойству параллелограмма, угол HBA является вертикальным углом к углу BDC (так как AD || BC), поэтому угол HBA = m(BDC).

Таким образом, мы имеем уравнение:

m(HAB) = m(HBA) = m(BDC).

Исходя из этого, для нахождения m(ABH) нам нужно найти m(BDC).

Мы также знаем, что сумма углов в треугольнике равна 180°, поэтому углы BDC, HCD и m(BDH) должны в сумме равняться 180°:

m(BDC) + m(HCD) + m(BDH) = 180°.

Мы знаем, что m(HCD) = 20°, поэтому:

m(BDC) + 20° + m(BDH) = 180°.

Так как BH = AD, m(HBA) = m(ABH). Поэтому:

m(BDH) = m(HAB).

Используя это равенство, мы можем переписать уравнение:
m(BDC) + 20° + m(HAB) = 180°.

Теперь мы можем решить это уравнение, чтобы найти m(BDC).

m(BDC) + 20° + m(HAB) = 180°.

m(BDC) + m(HAB) = 180° - 20°.

m(BDC) + m(HAB) = 160°.

Так как m(HAB) = m(BDC), мы можем заменить m(HAB) на m(BDC):

2m(BDC) = 160°.

m(BDC) = 160° / 2.

m(BDC) = 80°.

Поскольку m(BDC) = m(HAB), мы можем найти m(ABH):

m(ABH) = m(BDC) = 80°.

Итак, ответ на вопрос "Найдите m(ABH)" составляет 80°.