ХЕЛП 8 КЛАСС ГЕОМЕТРИЯ
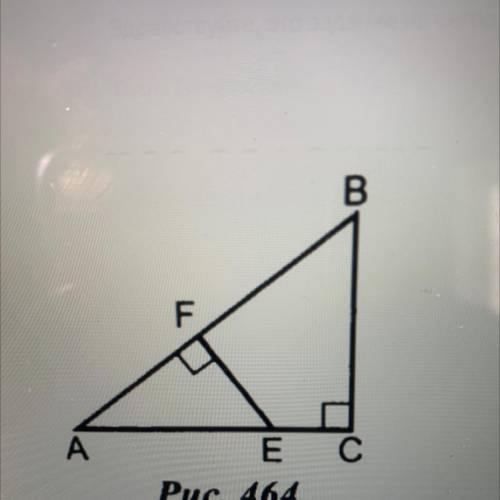
ВС перпендикулярна АС, EF перпендикулярна AB, BC=12, EF=6,AE=10. Найти AB

ХЕЛП 8 КЛАСС ГЕОМЕТРИЯ ВС перпендикулярна АС, EF перпендикулярна AB, BC=12, EF=6,AE=10. Найти AB

Ответы

ReyCh23 20.02.2021 16:13

AB=20

ΔАВС ~ ΔАЕF по первому признаку подобия( ∠С=∠F, ∠А- общий)

$\frac{BC}{EF}=\frac{AB}{AE};\\\\AB*EF= DC*AE;$

$AB=\frac{BC*AE}{EF}=\frac{12*10}{6}=20$

ПОКАЗАТЬ ОТВЕТЫ

Goodmegaparadise 18.01.2024 12:13

Для решения данной задачи, нам понадобятся знания о перпендикулярности и треугольниках.

Посмотрим на треугольник АВС. У нас даны две перпендикулярные прямые, ВС и EF. Так как ВС перпендикулярна АС, то угол АСВ является прямым углом. Также, так как EF перпендикулярна АВ, то угол АВF также является прямым углом.

Теперь воспользуемся свойством треугольника: сумма углов в треугольнике равна 180 градусов.

У нас уже есть два прямых угла: АСВ и АВF. Поэтому, угол В также равен 90 градусам.

Так как теперь у нас известен угол БВА (90 градусов) и длина стороны ВС (12), мы можем использовать теорему Пифагора для нахождения длины стороны АБ.

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, мы можем записать уравнение: AB^2 = BC^2 - AC^2.

Мы знаем, что BC = 12 и AC = AE - EC = 10 - 6 = 4.

Подставим значения в уравнение: AB^2 = 12^2 - 4^2 = 144 - 16 = 128.

Возьмем квадратный корень и найдем длину стороны АБ: AB = sqrt(128) = 11.3137 (округлим до четырех знаков после запятой).

Окончательный ответ: длина стороны АБ составляет около 11.3137 единиц.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия