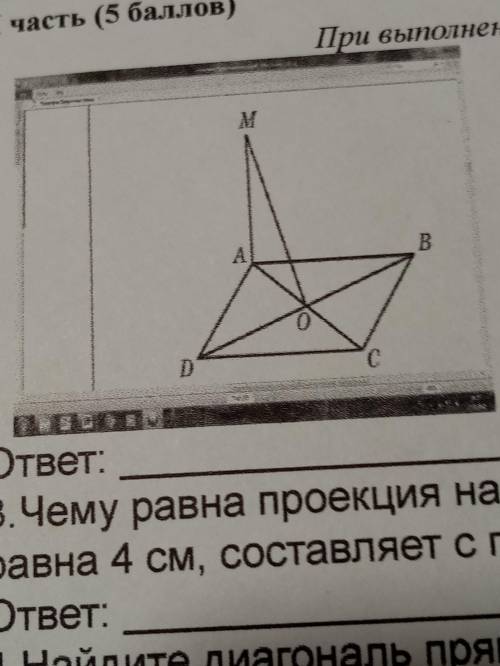
Геометрия,, К плоскости ABCD проведения перпендикуляр MA.(см. рис)

1. Какой из прямых (DM, BM, OM) перпендикулярна прямая DB?
2. Какой из плоскостей (DAM, DAB, ABM) перпендикулярна плоскость MAO?
3. Чему равна проекция наклонной на плоскость, если наклонная, длина которой равна 4 см, составляет с плоскостью угол 30 градусов?
4. Найдите диагональ прямоугольного параллелепипеда, измерения которого равны 2 см, 4 см, 4 см.
5. В кубе ABCDA1B1C1D1 найдите угол между плоскостями ABC и CDA1.

1. Чтобы определить, какая из прямых (DM, BM, OM) перпендикулярна прямой DB, нужно изучить свойство перпендикулярности. Две прямые называются перпендикулярными, если они пересекаются и образуют прямой угол (угол, равный 90 градусам).

Из рисунка видно, что прямая DB пересекает прямые DM и BM, образуя прямой угол. Однако, прямая DB не пересекает прямую OM. Поэтому мы можем заключить, что прямые DM и BM перпендикулярны прямой DB, а прямая OM не является перпендикулярной прямой DB.

2. Чтобы определить, какая из плоскостей (DAM, DAB, ABM) перпендикулярна плоскости MAO, вновь используем свойство перпендикулярности. Две плоскости называются перпендикулярными, если их нормальные векторы перпендикулярны.

Для начала найдем нормальный вектор для плоскости MAO. Вектор MA направлен из точки M в точку A, а вектор AO направлен из точки A в точку O. Нормальный вектор плоскости MAO можно получить как векторное произведение векторов MA и AO.

Вектор MA: MA = (A - M) = (3 - 1, 2 - 4, 3 - 3) = (2, -2, 0)
Вектор AO: AO = (O - A) = (1 - 3, 5 - 4, 2 - 3) = (-2, 1, -1)

Теперь найдем векторное произведение MA и AO:
MAO = MA x AO = (2, -2, 0) x (-2, 1, -1)
= (-2*(-1) - 0*1, 2*(-1) - 0*(-2), 2*1 - (-2)*(-2))
= (2, -2, 6)

Таким образом, нормальный вектор плоскости MAO равен (2, -2, 6).

Теперь рассмотрим плоскости DAM, DAB и ABM. Чтобы определить, какая из них перпендикулярна плоскости MAO, нужно проверить, перпендикулярны ли их нормальные векторы.

Нормальный вектор плоскости DAM равен (0, -3, 2).
Нормальный вектор плоскости DAB равен (-1, 0, 2).
Нормальный вектор плоскости ABM равен (0, 1, -4).

Теперь проверим перпендикулярность нормальных векторов:
MAO * DAM = (2, -2, 6) * (0, -3, 2) = 0 + 6 + 12 = 18
MAO * DAB = (2, -2, 6) * (-1, 0, 2) = -2 + 0 + 12 = 10
MAO * ABM = (2, -2, 6) * (0, 1, -4) = -2 - 12 - 12 = -26

Исходя из этих результатов, мы можем заключить, что плоскость DAM перпендикулярна плоскости MAO.

3. Чтобы определить проекцию наклонной на плоскость, нужно использовать формулу проекции вектора на плоскость:

Проекция = (Вектор * Нормальный вектор плоскости) / Длина нормального вектора плоскости

В данном случае, нам дана длина наклонной (4 см) и угол между наклонной и плоскостью (30 градусов). Нам также нужна нормальная величина плоскости. Вычислим нормальный вектор плоскости, используя угол, под которым наклонная пересекает плоскость.

Длина наклонной: AB = 4 см
Угол между наклонной и плоскостью: θ = 30 градусов

Так как нам известны два катета прямоугольного треугольника (AB и AC), мы можем использовать формулу тангенса, чтобы найти нормальный вектор плоскости:

tan(θ) = AC / AB
tan(30) = AC / 4
1/sqrt(3) = AC / 4
AC = 4/sqrt(3) см

Теперь у нас есть длина нормального вектора плоскости (AC). Давайте найдем его направление. Мы можем взять стандартный ортогональный базис для плоскости (x, y, z) и задать единичные векторы для каждой из осей:

(i, j, k) = (1, 0, 0), (0, 1, 0), (0, 0, 1)

Теперь объединим единичные векторы с соответствующими коэффициентами для получения нормального вектора плоскости:

нормальный вектор плоскости = AC • (i / Длина вектора AC) + 0 • (j / Длина вектора AC) + 0 • (k / Длина вектора AC)
нормальный вектор плоскости = AC/Длина вектора AC • i = (4/sqrt(3))/4 • (1, 0, 0) = (1/sqrt(3), 0, 0)

Теперь у нас есть нормальный вектор плоскости (1/sqrt(3), 0, 0).

Наконец, чтобы найти проекцию наклонной на плоскость, мы можем использовать формулу проекции:

Проекция = (AB • нормальный вектор плоскости) / Длина нормального вектора плоскости
Проекция = (4 см • (1/sqrt(3), 0, 0)) / (1/sqrt(3))
Проекция = 4 см • (1, 0, 0)
Проекция = 4 см

Таким образом, проекция наклонной на плоскость равна 4 см.

4. Чтобы найти диагональ прямоугольного параллелепипеда, мы можем использовать теорему Пифагора. Теорема Пифагора гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. В случае прямоугольного параллелепипеда, диагональ является гипотенузой, а измерения равны катетам.

Измерения прямоугольного параллелепипеда: a = 2 см, b = 4 см, c = 4 см

Теперь мы можем использовать формулу теоремы Пифагора для найти диагональ:

диагональ = sqrt(a^2 + b^2 + c^2)
диагональ = sqrt((2 см)^2 + (4 см)^2 + (4 см)^2)
диагональ = sqrt(4 см^2 + 16 см^2 + 16 см^2)
диагональ = sqrt(36 см^2)
диагональ = 6 см

Таким образом, диагональ прямоугольного параллелепипеда равна 6 см.

5. Чтобы найти угол между плоскостями ABC и CDA1 в кубе ABCDA1B1C1D1, мы можем использовать свойство перпендикулярности между нормальными векторами плоскостей.

Нормальный вектор плоскости ABC равен (0, 0, 1) (так как плоскость параллельна оси Z).
Нормальный вектор плоскости CDA1 равен (0, -1, 0) (так как плоскость параллельна оси Y).

Теперь можно найти угол между нормальными векторами плоскостей, используя скалярное произведение:

cos(θ) = (нормальный вектор ABC • нормальный вектор CDA1) / (Длина нормального вектора ABC * Длина нормального вектора CDA1)
cos(θ) = (0*0 + 0*(-1) + 1*0) / (sqrt(0^2 + 0^2 + 1^2) * sqrt(0^2 + (-1)^2 + 0^2))
cos(θ) = 0 / (1 * 1)
cos(θ) = 0

Таким образом, угол между плоскостями ABC и CDA1 равен 0 градусов. Это означает, что плоскости ABC и CDA1 являются параллельными.