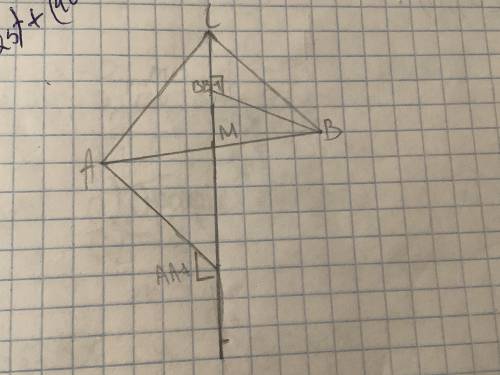
Геометрия дано: треугольник ABC, СМ — медиана, АА1 перпендикулярна СМ, ВВ1 перпендикулярна СМ.
доказать: АА1=ВВ1
Другие вопросы по теме Геометрия
Популярные вопросы
- САБАҚ математика ВИДЕОКОНФЕРЕНЦИЧат ашу –IIIШеңбер, дөңгелек және олардыңэлементтеріБос...
1 - хелп ми : надо подставить фразы...
2 - Как называется сборник, в который входит повесть Барышня-крестьянка ? * Дубровский...
1 - СКОЛЬКО БУДЕТ 82829+728189÷0=...
2 - Киіз үйдің бөліктері. * Сыртқы бөлігіОшақІшкі бөлігіСүйектері, киіздері, бау-шуларыкөмек...
3 - -x2+2x+3 опишите свойства квадратичной функции...
2 - В одной из школ технического творчества занимался студент-математик несколько лет,...
1 - Определите и запишите основную мысль текста ...
3 - Өлеңдегі автор ойын және өлеңнің тәрбиелік мәнін жазыңдар...
2 - Complete the mini-dialogues with the words in the box...
3
По определению медианы, точка М делит сторону AC пополам. Это означает, что AM = MC.
Также, по определению перпендикуляра, линия АА1 перпендикулярна к линии СМ и линия ВВ1 перпендикулярна к линии СМ. Значит, углы AAM и VVM являются прямыми углами (равны 90 градусам).
Давайте рассмотрим треугольник AAM. У нас есть следующая информация:
- Угол ААМ равен 90 градусам (по определению перпендикуляра)
- Сегмент АМ равен СМ (по определению медианы)
- Угол АМА1 является прямым углом (равен 90 градусам)
Таким образом, треугольник AAM является прямоугольным треугольником с двумя сторонами, равными AM.
Аналогично, рассмотрим треугольник VVM. У нас есть следующая информация:
- Угол ВВМ равен 90 градусам (по определению перпендикуляра)
- Сегмент ВМ равен СМ (по определению медианы)
- Угол ВМВ1 является прямым углом (равен 90 градусам)
Таким образом, треугольник VVM является прямоугольным треугольником с двумя сторонами, равными VM.
Из этой информации мы можем заключить, что AM = AA1 и VM = VV1, так как это стороны прямоугольных треугольников и они равны гипотенузам.
Таким образом, мы можем утверждать, что АА1 = ВВ1, так как AM = AA1 и VM = VV1, и оба значения равны сегменту СМ (по определению медианы).
Это доказывает, что АА1 и ВВ1 равны друг другу.